Chapter 10 – Straight Lines (Ex – 10.3)

Straight Lines (Ex – 10.3)

Question 1.
Reduce the following equations into slope- intercept form and find their slopes and the y-intercepts.
(i) x + 7y = 0,
(ii) 6x + 3y-5 = 0,
(iii) y=0

Solution:

Question 2.
Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0,
(ii) 4x – 3y = 6,
(iii) 3y + 2 = 0

Solution:

Question 3.
Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.

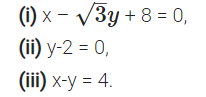
Solution:

Question 4.
Find the distance of the point (-1, 1) from the line 12 (x+ 6) = 5(y — 2).

Solution:

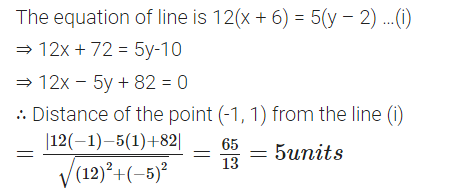
Question 5.
Find the points on the x-axis, whose distances from the line x/3 + y/4 =1 are 4 units.

Solution:

Question 6.
Find the distance between parallel lines
(i) 15x+8y-34 = 0and 15x + 8y+31 =0
(ii) |(x + y) + p = 0 and |(x + y) – r = 0.

Solution:
If lines are Ax + By + Q = 0
and Ax + By + C₂ = 0, then distance between

Question 7.
Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (-2, 3).

Solution:
We have given an equation of line 3x – 4y + 2 = 0
Slop of the line(i) = 3/4
Thus, slope of any line parallel to the given line (i) is 3/4 and passes through (-2, 3), then its equation is

Question 8.
Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.

Solution:
Given equation is x – 7y + 5 = 0 … (i)
Slope of this line = 1/7
∴ Slope of any line perpendicular to the line (i) is -7 and passes through (3, 0) then
y – 0 = -7(x – 3)
[∵ Product of slope of perpendicular lines is -1]
⇒ y = -7x + 21
⇒ 7x + y – 21 = 0, is the required equation of line.

Question 9.

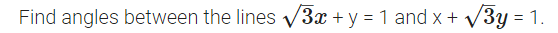
Solution:

Question 10.
The line through the points (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0 at right angle. Find the value of h.

Solution:
Given points are (h, 3) and (4,1).
∴ Slope of the line joining (h, 3) & (4,1)

Question 11.
Prove that the line through the point (x₁ y₁) and parallel to the line Ax + By + C = 0 is A(x-x₁) + B(y-y₁) = 0.

Solution:

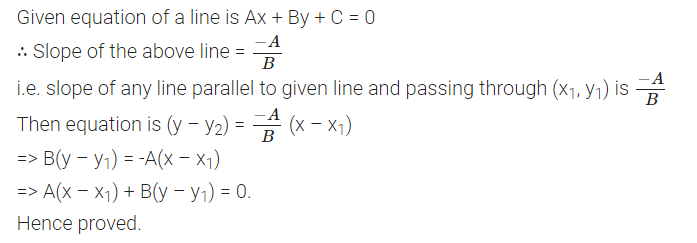
Question 12.
Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find equation of the other line.

Solution:
We have given a point (2, 3), through which two lines are passing and intersects at an angle of 60°.
Let m be the slope of the other line

Question 13.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (-1, 2).

Solution:
suppose the given points are A and B.
Let M be the mid point of AB.

Question 14.
Find the coordinates of the foot of perpendicular from the point (-1, 3) to the line 3x – 4y – 16 = 0.

Solution:
We have, 3x – 4y – 16 = 0
Slope of the kine(i) = 3/4
Then equation of any line ⊥ from (-1, 3) to the given line(i) is

Question 15.
The perpendicular from the origin to the line y = mx + c meets it at the point (-1,2). Find the values of m and c.

Solution:

Given, the perpendicular from the origin to the line y = mx + c meets it at the point (-1, 2)
∴ 2 = m (-1) + c … (i)
⇒ c – m = 2

Question 16.
If p and q are the lengths of perpendiculars from the origin to the lines x cosθ – y sinθ = k cos 2θ and x secθ + y cosecθ = k, respectively, prove that p² + 4q² = k².

Solution:
Given p and q are the lengths of perpendiculars from the origin to the lines x cos θ – ysinθ=k cos 2θ and xsecθ+y cosec θ = k.

Question 17.
In the triangle ABC with vertices A(2, 3), 8(4, -1) and C( 1, 2), find the equation and length of altitude from the vertex A.

Solution:
We have given a AABC with the vertices, A (2, 3), B (4, -1) and C (1, 2)

Question 18.

Solution:
Given, p be the length of perpendicular from the origin to the line whose intercepts