Pair of Linear Equations in Two Variables
Question 1.
Solve the following pair of linear equations by the elimination method and the substitution method:
- x + y = 5 and 2x – 3y = 4
- 3x + 4y = 10 and 2x – 2y = 2
- 3x – 5y – 4 = 0 and 9x = 2y + 7
- x/2 + 2y/3 = – 1 and x – y/3 = 3
Solution:
1. By elimination method:
The given system of equations is
x +y = 5 ……………….. (1) and
2x – 3y = 4 ………………….. (2)
Multiplying (1) by 3, we get
3x + 3y = 15 ……………….. (3)
Adding (2) and (3), we get
5x = 19
or x = 19/5
Putting x = 19/5 in (1), we get
19/5 + y = 5
or y = 5 – 19/5
or y = (25−19)/5
or y = 6/5
Hence, x = 19/5, y = 6/5.
By substitution method:
The given system of equations is
x + y = 5 ……………. (1) and
2x – 3y = 4 ……………….. (2)
From (1), y = 5 – x
Substituting y = 5 – x in (2), we get
2x – 15 + 3x = 4
or 5x = 4 + 15
or 5x = 19
or x = 19/5
Putting x = 19/5 in (1), we get
19/5 + y = 5
or y = 5 – 19/5
or y = (25−19)/5
or y = 6/5
Hence, x = 19/5, y = 6/5.
2. By elimination method:
The given system of equations is
3x + 4y = 10 ……………… (1)
and 2x – 2y = 2 ………………. (2)
Multiplying (2) by 2 and adding to (1), we get
7x = 14
or x = 2
Putting x = 2 in (2), we get
2(2) – 2y = 2
or – 2y = 2 – 4
or -2y = -2
or y = 1
Hence, x = 2, y = 1
By substitution method:
The given system of equations is
3x + 4y = 10 ……………….. (1)
and 2x – 2y = 2
or x – y = 1 …………….. (2)
From (2), Putting y = x – 1 in (1), we get
3x + 4(x – 1) = 10
or 3x + 4x – 4 = 10
or 7x = 14
or x = 2
Putting x = 2 in (2), we get
2 – y = 1
or – y = 1 – 2
or – y = – 1
or y = 1
Hence, x = 2, y = 1
3. By elimination method:
The given system of equations is
3x – 5y – 4 = 0
or 3x – 5y = 4 ……………….. (1)
and 9x = 2y + 7
or 9x – 2y = 7 ………………….. (2)
Multiplying (1) by 3 , we get
9x – 15y = 12 ………………. (3)
Substracting (3) & (2), we get
– 13y = 5
or y = – 5/13
Putting y = – 5/13 in (1), we get
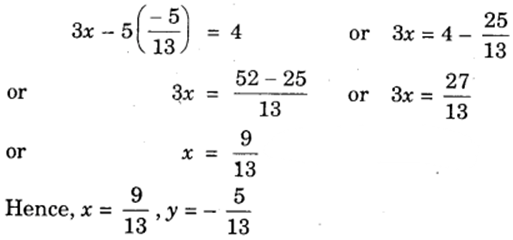
By substitution method:
The given system of equations is

4. By elimination method:
The given system of equations is

Multiplying (2) by 4 and adding to (1), we get
15x = 30
or x = 2
Putting x = 2 in (2), we get
3(2) – y = 9
or – y = 9 – 6
or – y = 3
y = – 3
By substitution method:
The given system of equations is

From (2), putting y = 3x – 9 in (1), we get y = 3x – 9
3x + 4(3x – 9) = – 6
or 3x + 12x – 36 = – 6
or 15x = 30
x = 2
Putting x = 2 in (2), we get
3(2) – y = 9
or – y = 9 – 6
or – y = 3
or y = – 3
Hence, x = 2, y = – 3.
Question 2.
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method:
1. If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to the denominator. What is the fraction?
2. Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
3. The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
4. Meena went to a bank to withdraw Rs 2000. She asked the cashier to give her Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes of Rs 50 and Rs 100 she received.
5. A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs 27 for a book she kept for seven days, while Susy paid Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Solution:
1. Let x be the numerator and y be the denominator of the fraction. So, the fraction is x/y.
By given conditions:
(x+1)/(y−1) = 1
or x + 1 = y – 1
or x – y = – 2 ……………….. (1)
and x/y+1 = 1/2
or 2x = y + 1
or 2x – y = 1 ……………….. (2)
Subtracting (2) from (1), we get
(x – y) – (2x – y) = – 2 – 1
or x – y – 2x + y = – 3
or – x = – 3
or x = 3
Substituting x = 3 in (1), we get
3 – y = – 2
or y = 5
Hence, the required fraction is 3/5.
2. Let the present age of Nuri be x years
and the present age of Sonu be y years.
Five years ago,
Nuri’s age = (x – 5) years
Sonu’s age = (y – 5) years
As per conditions,
x – 5 = 3(y – 5)
or x – 5 = 3y – 15
or x – 3y = – 15 + 5
or x – 3y = – 10 ………………… (1)
Ten years later,
Nuri’s age = (x + 10) years
As per condition’s,
x + 10 = 2 (y + 10)
or x + 10 = 2y + 20
or x – 2y = 20 – 10
or x – 2y = 10 ………………… (2)
Putting y = 20 in (2), we get
x – 2(20) = 10
or x = 10 + 40 = 50
Nuri’s present age = 50 years
and Sonu’s present age = 20 years
3. Let the digits in the unit’s place and ten’s place be x and y respectively.
∴ Number = 10y + x
If the digits are reversed, the new number = 10y + x
As per conditions:
x + y = 9 ……………… (1)
and 9(10y + x) = 2(10x + y)
or 90y + 9x = 20x + 2y
or 20x – 9x + 2y – 90y = 0
From (1), y = 9 – x
Putting y = 9 – x in (2), we get
11x – 88(9 – x) = 0
or 11x – 88 × 9 + 88x = 0
or 99x = 88 × 9
Putting x = 8 in (1), we get
8 + y = 9
or y = 1
Hence, the number = 10y + x = 10 × 1 + 8 = 18
4. Let the number of Rs 50 notes be x and number of Rs 100 notes be y. Then,
x + y – 25 …………….. (1)
and 50x + 100y = 2000
or x + 2y = 40 …………….. (2)
On subtracting (1) from (2), we get
y = 15
Putting y = 15 in (1), we get
x + 15 = 25
or x = 10
Hence, number of Rs 50 notes = 10
and number of Rs 100 notes = 15
5. Let the fixed charges for 3 days be Rs x and charges per day be Rs y.
∴ By the given conditions,
x + 4y = 27 ………….. (1)
and x + 2y = 21 ……………… (2)
Subtracting (2) from (1), we get
2y = 6
or y = 3
Putting y = 3 in (1), we get
x + 4 × 3 = 27
or x = 27 – 12
x = 15
∴ Fixed charges = Rs 15 and
charges per day = Rs 3
