Chapter 8 – Introduction to Trigonometry (Ex – 8.4)

Introduction to Trigonometry

Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

Solution:
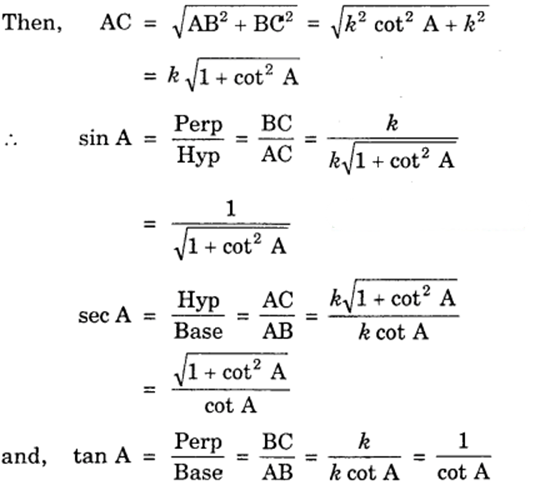
Consider a ∆ ABC, in which ∠B = 90°.

Base = AB
Perp. = BC
and Hyp. = AC
∴ cot A =  Base/Perp  = AB/BC
or AB/BC = cot A = cotA/1
Let AB = k cot A and BC = k.

Question 2.
Write the other trigonometric ratios of A in terms of sec A.

Solution:
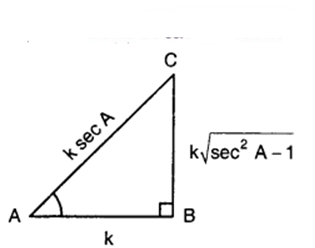
Consider a ∆ ABC, in which ∠B = 90°

For ∠A, we have :
Base = AB,
Perp = BC
Hyp = AC.
∴ sec A =  Hyp/Base  = AC/AB
or AC/AB = sec A = secA/1
Let AB = k and AC = k sec A.

Question 3.
Evaluate :
(i) (sin²63^∘+sin²27^∘)/(cos²17^∘+cos²73^∘)
(ii) sin 25° cos 65° + cos 25° sin 65°

Solution:
(i) Here, sin 63° = sin (90° – 27°) = cos 27°
and cos 17° = cos (90° – 73°) = sin 73°

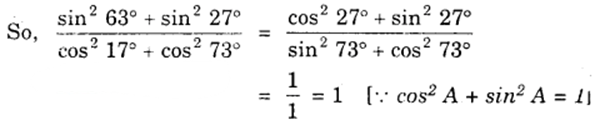
(ii) sin 25° cos 65° + cos 25° sin 65°
= sin (90° – 65°) cos 65° + cos (90° – 65°) sin 65°
= cos 65° cos 65° + sin 65° sin 65°
= cos² 65° + sin² 65°
= 1

Question 4.
Choose the correct option. Justify your choice :
(i) 9 sec² A – 9 tan² A =
(A) 1
(B) 9
(C) 8
(D) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) none of these

(iii) (sec A + tan A)(1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A

(iv) 1+tan2A1+cot2A
(A) sec² A
(B) – 1
(C) cot² A
(D) none of these

Solution:
(i) (B), because
9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9 x 1
= 9

(ii) (C), because
(1 + tan θ + sec θ )(1 + cot θ – cosec θ)

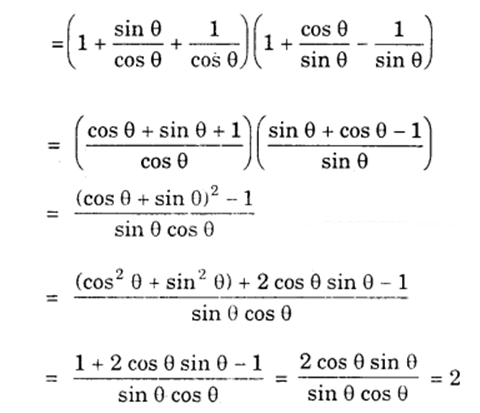
(iii) (D), because
(sec A + tan A)(1 – sin A) =

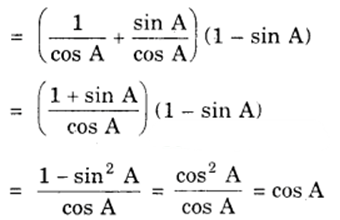
(iv) (D), because

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined :

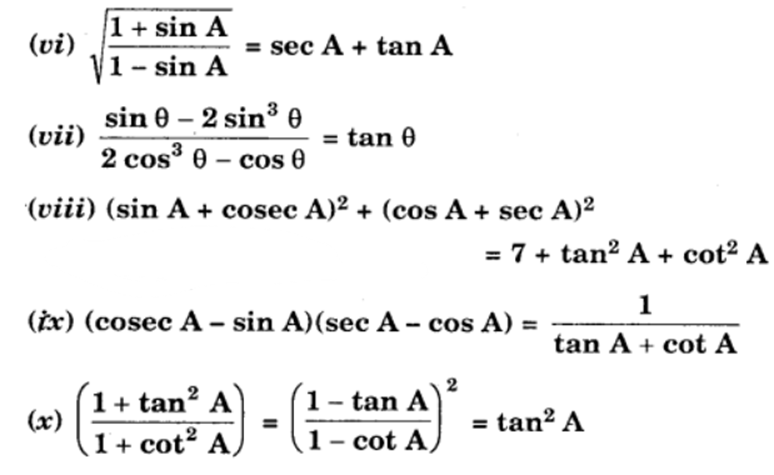
Solution:
(i) We have :
L.H.S. = (cosec θ – cot θ)²

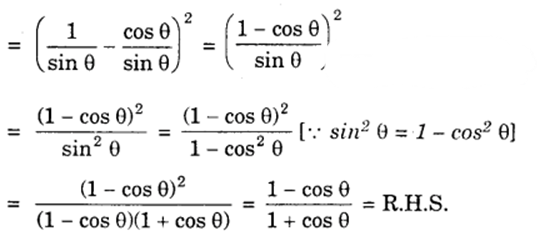
(ii) We have :

(iii) We have :

(iv) We have :

(v) We have :

(vi) We have :

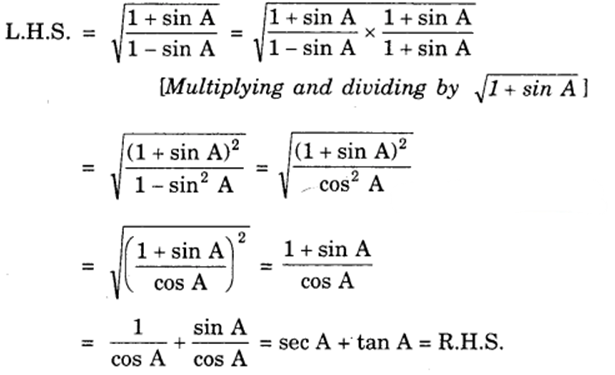
(vii) We have :

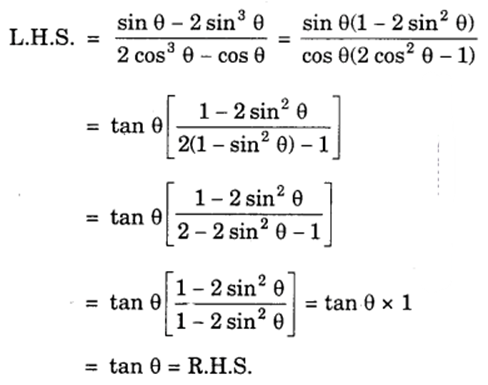
(viii) We have :
L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= (sin² A + cosec² A + 2 sin A cosec A) + (cos² A + sec2 A + 2 cos A sec A)
= (sin² A + cosec² A + 2 sin A.1/sinA) + (cos² A + sec2 A + 2 cos A. 1/cosA)
= (sin²A + cosec² A + 2) + (cos² A + sec² A + 2)
= sin²A + cos² A + cosec² A + sec² A + 4
= 1 + (1 + cot² θ) + (1 + tan² A) + 7 + tan² A + cot² A [ ∵ cosec² A = 1 + cot² A and sec² A = 1 + tan² A]
= R.H.S.

(ix) We have :

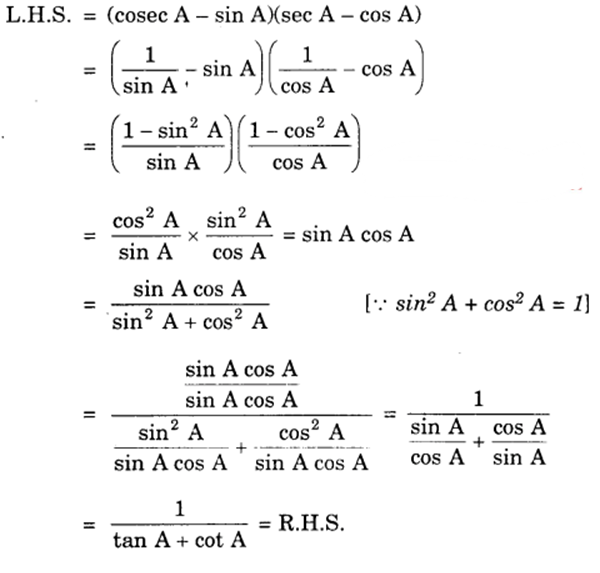
(x) We have :