Areas Related to Circles
Question 1.
Find the area of the shaded region in the figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
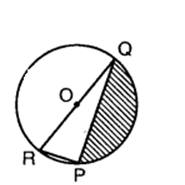
Solution:
Since ROQ is a diameter, therefore ∠RPQ = 90°.
RQ² = RP² + PQ²
or RQ² = 7² + 24²
or RQ² = 49 + 576
or RQ² = 625
or RQ = √625 cm
∴ RQ = 25 cm
∴ Radius r = 1/2 RQ = 25/2 cm

Question 2.
Find the area of the shaded region in the figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
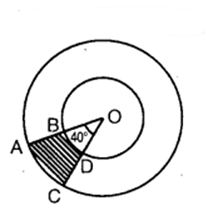
Solution:
Area of the shaded region = Area of sector AOC – Area of sector OBD
Question 3.
Find the area of the shaded A region in the figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
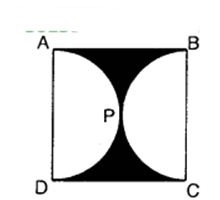
Solution:
Area of the square ABCD = (14)² cm² = 196 cm²
Diameter of the semicircles = AD or BC = 14 cm
∴ Radius of each semicircle = 14/2 cm = 7 cm
∴ Area of the both semicircular regions
= 2 x 1/2 πr² = πr²
= (22/7 x 49) cm² = 154 cm²
∴ Area of the shaded regions = Area of the square ABCD – Area of the both semicircular regions
= (196 – 154) cm² = 42 cm².
Question 4.
Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
Solution:
Area of the circular portion
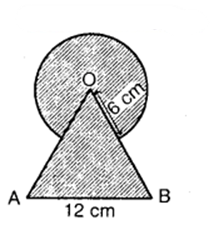
Area of the equilateral ∆ OAB
√3/4(side)² = (√3/4 x 144) cm²
= 36√3 cm²
Area of the shaded region = Area of circular portion + Area of the equilateral triangle
= (660/7+36√3) cm²
Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.
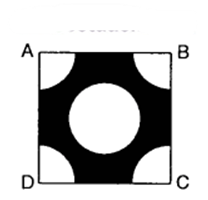
Solution:
The area of the square ABCD = (side)²
= 4² cm²
= 16 cm²
The sum of the areas of the four quadrants at the four corners of the square
= The area of a circle of radius 1 cm
= 22/7 x 1² cm²
= 22/7 cm²
The area of the circle of diameter 2 cm, i.e., radius 1 cm²
= 22/7 x 1² cm²
= 22/7 cm²
Area of the remaining portion of the square = The area of the square ABCD – The sum of the areas of 4 quadrants at the four corners of the square – The area of the circle of diameter 2 cm
= (16 – 22/7 – 22/7) cm²
= {(112−22−22)/7} cm²
= 68/7 cm²
= 9.71 cm²
Question 6.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the figure. Find the area of the design (shaded region).
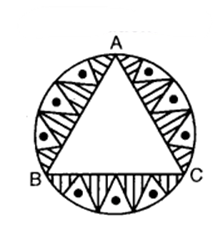
Solution:
Let ABC be an equilateral triangle and let 0 be the circumcentre of the circumcircle of radius 32 cm.
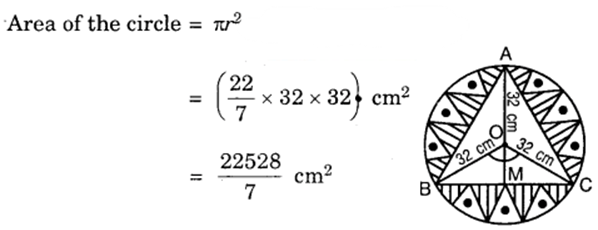
Draw OM ⊥ BC.
Now, ∠BOM = 1/2 x 120° = 60°
So, from ∆ BOM, we have

Hence, area of ∆ BOC
= 1/2 BC x OM
= 1/2 x 32√3 x 16 cm²
Area of ∆ ABC = 3 x Area of ∆ BOC
= (3 x 1/2 x 32√3 x 16) cm²
= 768√3 cm²
∴ Area of the design (i.e., shaded region) = Area of the circle – Area of ∆ ABC
= (22528/7−768√3) cm²
Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
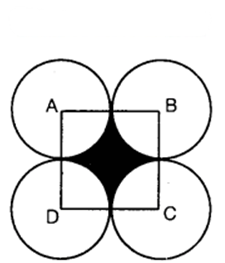
Solution:
The area of the square ABCD = (side)² = 142 cm²
= 196 cm².
The sum of the areas of the four quadrants at the four corners of the square
= The area of a circle of radius 14/2 cm = 7 cm²
= π(7)² cm² =(22/7 x 49) cm² = 154 cm²
Area of the shaded region = The area of the square ABCD – The sum of the areas of four quadrants at the four corners of the square
= (196 – 154) cm² = 42 cm²
Question 8.
Figure depicts a racing track whose left and right ends are semicircular.

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find
(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:
We have OB = O’C = 30 m
and, AB = CD = 10 m
OA = O’D = (30 + 10) m = 40 m
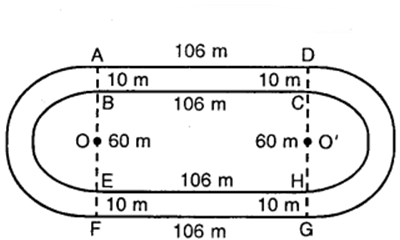
(i) the distance around the track along its inner edge.
= BC + EH + 2 x circumference of the semicircle of radius OB = 30 m
= ( 106 + 106 + 2 x 1/2 x 2π(30) ) m
= ( 212 + 2 x 22/7 x 30) m
= ( 212 + 1320/7 )m
= {(1484+1320)/7} m
= 2804/7 m
= 400.57 m
(ii) Area of the track = Area of the shaded region = Area of rectangle ABCD + Area of rectangle EFGH + 2(Area of the semicircle of radius 40 m – Area of the semicircle with radius 30 m)
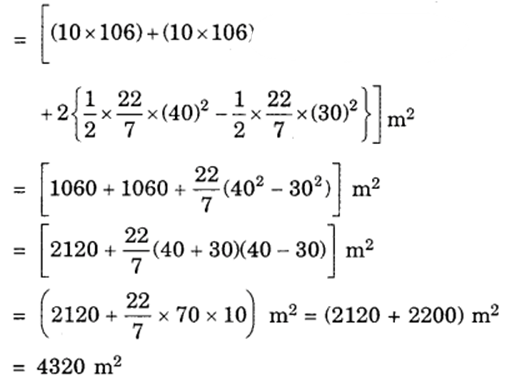
Question 9.
In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
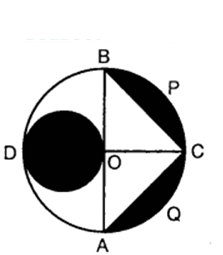
Solution:
Area of the sector OCB = (90∘/360∘ × 22/7 × 7 × 7) cm²
= 77/2 cm²
Area of ∆ OCB = 1/2 x OC x OB
= 1/2 x 7 x 7 cm²
= 49/2 cm²
The area of the segment BPC = Area of the sector OCB – Area of the A OCB
= (77/2 – 49/2) cm²
= 28/2 cm²
= 14 cm²
Similarly, the area of the segment AQC
= 14 cm²
Also,the area of the circle with DO as diameter
= (22/7 x 7/2 x 7/2) cm² = 77/2 cm²
Hence,the total area of the shaded region
= (14 + 14 + 77/2) cm²
= {(28+28+77)/2} cm²
= 133/2 cm²
= 66.5 cm²
Question 10.
The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region.
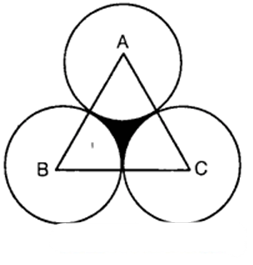
(Use π = 3.14 and 3–√ = 1.73205)
Solution:
Let each side of the triangle be a cm. Then,
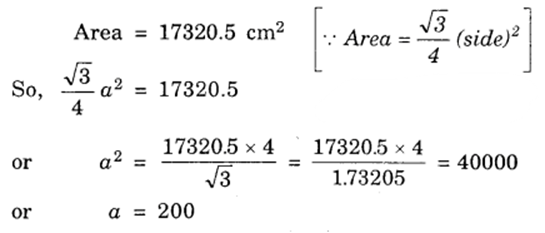
Thus, radius of each circle is 200/2 cm = 100 cm.
Now, area of shaded region
= Area of ∆ ABC – 3 x (Area of a sector of angle 60° in a circle of radius 100 cm)
= [17320.5 – 3(60∘/360∘ x 3.14 x 100 x 100)] cm²
= (17320.5 – 15700) cm²
= 1620.5 cm²
Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.
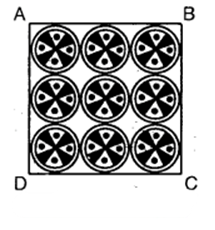
Solution:
Side of the square ABCD
= AB – 3 x diameter of circular design
= 3 x (2 x 7) cm – 42 cm
∴ Area of the square ABCD
= (42 x 42) cm² = 1764 cm²
Area of one circular Resign
= πr² = (22/7 x 7 x 7) cm²
= 154 cm²
∴ Area of 9 such designs
= (9 x 154) cm² = 1386 cm²
∴ Area of the remaining portion of the handkerchief
= Area of the square ABCD – Area of 9 circular designs
= (1764 – 1386) cm²
= 378 cm²
Question 12.
In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
Solution:

Hence, area of the shaded region = Area of quadrant – Area of ∆ BOD
= (77/8 – 7/2) cm² = {(77−28)8} cm²
= 49/8 cm²
= 6.125 cm²
Question 13.
In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)

Solution:
Radius of the quadrant = OB = √(OA2+AB2)
= √(202+202) cm
= 20√(1+1) cm
= 20√2 cm
∴ Area of quadrant OPBQ
= 1/4πr²
= 1/4 x 3.14 x (20√2)² cm²
= ( 1/4 x 3.14 x 800) cm²
= 628 cm²
Area of the square OABC = (20) cm² = 400 cm²
Hence, area of the shaded region = Area of quadrant – Area of square OABC
= (628 – 400) cm² = 228 cm².
Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB = 30°, find the area of the shaded region.
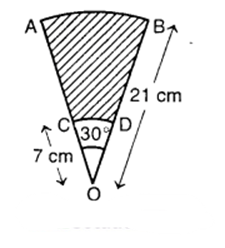
Solution:
Let A1 and A2 be the areas of sector OAB and OCD respectively. Then,
A1 = Area of a sector of angle 30° in a circle of radius 21 cm
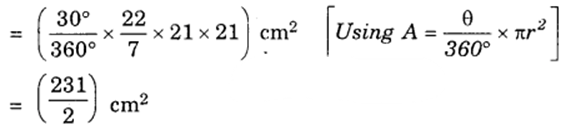
A2 = Area of a sector of angle 30° in a circle of radius 7 cm

Question 15.
In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
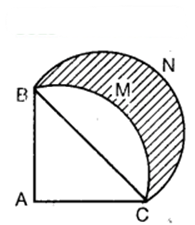
Solution:
Here the radius of the quadrant with A as the centre is 14 cm.
Then, the area of the quadrant ABMC
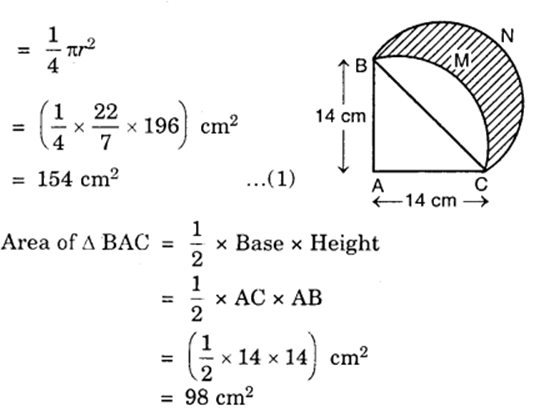
Area of the segment BMC of the circle = Area of the quadrant ABMC – Area of ∆ BAC
= (154 – 98) cm²
= 56 cm²
Now, since AC = AB = 14 cm and ∠BAC = 90°, therefore by Pythagoras Theorem,
BC = √(AC2+AB2)
= √(142+142)
= 14√2 cm
∴ Radius of the semicircle BNC = 1/2 x 14√2 cm = 7√2 cm
∴ Area of the semicircle BNC
= (7√2 )² cm²
= (1/2×22/7×98) cm² = 154 cm²
Hence, the area of the shaded region
= the area of the region between two arcs BMC and BNC = The area of semicircle BNC – The area of the segment of the circle BMC
= (154 – 56) cm²
= 98 cm²
Question 16.
Calculate the area of the designed region in figure common between the two quadrants of circles of radius 8 cm each.
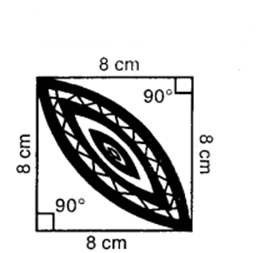
Solution:
Here, 8 cm is the radius of each of the quadrants ABMD and BNDC.
Sum of their areas
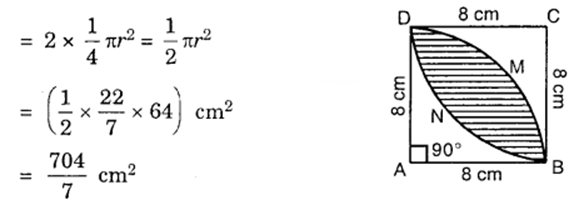
Area of the square ABCD = (8 x 8) cm² = 64 cm²
Area of the designed region = Area of the shaded region
= Sum of the areas of quadrants – Area of the square ABCD
= (704/7−64) cm² = {(704−448)/7} cm²
= 256/7 cm²
= 36.57 cm²
