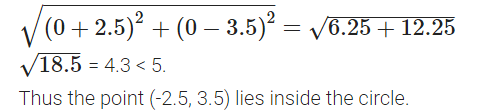Chapter 11 – Conic Sections (Ex – 11.1)

Conic Sections (Ex – 11.1)

In each of the following Exercises 1 to 5, find the equation of the circle with

Question 1.
center (0, 2) and radius 2

Solution:
Here h = 0,k = 2 and r = 2
The equation of circle is,
(x-h)² + (y- k)² = r²
∴ (x – 0)² + (y – 2)² = (2)²
⇒ x² + y² + 4 – 4y = 4
⇒ x² + y² – 4y = 0

Question 2.
center (-2,3) and radius 4

Solution:
Here h=-2, k = 3 and r = 4
The equation of circle is,
(x – h)² + (y – k)² = r²
∴( x + 2)² + (y – 3)² = (4)²
⇒ x² + 4 + 4x + y² + 9 – 6y = 16
⇒ x² + y² + 4x – 6y – 3 = 0

Question 3.
center (1/2,1/4) and radius 1/12

Solution:
here h = 1/2, k = 1/4 and r = 1/12
The equation of circle is,

Question 4.
center (1, 1) and radius √2

Solution:
Here h = l, k=l and r = √2
The equation of circle is,
(x – h)² + (y – k)² = r²
∴ (x – 1)² + (y – 1)² = (√2)²
⇒ x² + 1 – 2x + y² +1 – 2y = 2
⇒ x² + y² – 2x – 2y = 0

Question 5.
center (-a, -b) and radius √(a² − b²).

Solution:
Here h=-a, k = -b and r = √(a² − b²)
The equation of circle is, (x – h)² + (y – k)² = r²
∴ (x + a)² + (y + b)² = (√(a² − b²))
⇒ x² + a² + 2ax + y² + b² + 2by = a² -b²
⇒ x² + y² + 2ax + 2 by + 2b² = 0

In each of the following exercises 6 to 9, find the centre and radius of the circles.

Question 6.
(x + 5)² + (y – 3)² = 36

Solution:
The given equation of circle is,
(x + 5)² + (y – 3)² = 36
⇒ (x + 5)² + (y – 3)² = (6)²
Comparing it with (x – h)2² + (y – k)² = r², we get
h = -5, k = 3 and r = 6.
Thus the co-ordinates of the center are (-5, 3) and radius is 6.

Question 7.
x² + y² – 4x – 8y – 45 = 0

Solution:
The given equation of circle is
x² + y² – 4x – 8y – 45 = 0
∴ (x² – 4x) + (y² – 8y) = 45
⇒ [x² – 4x + (2)²] + [y² – 8y + (4)²] = 45 + (2)² + (4)²
⇒ (x – 2)² + (y – 4)² = 45 + 4 + 16
⇒ (x – 2)² + (y – 4)² = 65
⇒ (x – 2)² + (y – 4)²= (√65)2
Comparing it with (x – h)² + (y – k)² = r², we
have h = 2,k = 4 and r = √65.
Thus co-ordinates of the center are (2, 4) and radius is √65.

Question 8.
x² + y² – 8x + 10y – 12 = 0

Solution:
The given equation of circle is,
x² + y² – 8x + 10y -12 = 0
∴ (x² – 8x) + (y² + 10y) = 12
⇒ [x² – 8x + (4)²] + [y² + 10y + (5)²] = 12 + (4)² + (5)²
⇒ (x – 4)² + (y + 5)² = 12 + 16 + 25
⇒ (x – 4)² + (y + 5)² = 53
⇒ (x – 4)² + (y + 5)² = (53−−√)2
Comparing it with (x – h)² + (y – k)² = r², we have h = 4, k = -5 and r = √53
Thus co-ordinates of the center are (4, -5) and radius is √53.

Question 9.
2x² + 2y² – x = 0

Solution:
The given equation of circle is,
2x² + 2y² – x = 0

Question 10.
Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre is on the line 4x + y = 16.

Solution:
The equation of the circle is,
(x – h)² + (y – k)² = r² ….(i)
Since the circle passes through point (4, 1)
∴ (4 – h)² + (1 – k)² = r²
⇒ 16 + h² – 8h + 1 + k² – 2k = r²
⇒ h²+ k² – 8h – 2k + 17 = r² …. (ii)
Also, the circle passes through point (6, 5)
∴ (6 – h² + (5 – k)² = r²
⇒ 36 + h² -12h + 25 + k² – 10k = r²
⇒ h² + k² – 12h – 10kk + 61 = r² …. (iii)
From (ii) and (iii), we have h² + k² – 8h – 2k +17
= h² + k²– 12h – 10k + 61
⇒ 4h + 8k = 44 => h + 2k = ll ….(iv)
Since the center (h, k) of the circle lies on the line 4x + y = 16
∴ 4h + k = 16 …(v)
Solving (iv) and (v), we get h = 3 and k = 4.
Putting value of h and k in (ii), we get
(3)² + (4)² – 8 x 3 – 2 x 4 + 17 = r²
∴ r² = 10
Thus required equation of circle is
(x – 3)² + (y – 4)² = 10
⇒ x² + 9 – 6x + y² +16 – 8y = 10
⇒ x² + y² – 6x – 8y +15 = 0.

Question 11.
Find the equation of the circle passing through the points (2, 3) and (-1, 1) and whose center is on the line x – 3y – 11 = 0.

Solution:
The equation of the circle is,
(x – h)² + (y – k)² = r² ….(i)
Since the circle passes through point (2, 3)
∴ (2 – h)² + (3 – k)² = r²
⇒ 4 + h² – 4h + 9 + k² – 6k = r²
⇒ h²+ k² – 4h – 6k + 13 = r² ….(ii)
Also, the circle passes through point (-1, 1)
∴ (-1 – h)² + (1 – k)² = r²
⇒ 1 + h² + 2h + 1 + k² – 2k = r²
⇒ h² + k² + 2h – 2k + 2 = r² ….(iii)
From (ii) and (iii), we have
h² + k² – 4h – 6k + 13 = h² + k² + 2h – 2k + 2
⇒ -6h – 4k = -11 ⇒ 6h + 4k = 11 …(iv)
Since the center (h, k) of the circle lies on the line x – 3y-11 = 0.
∴ h – 3k – 11 = 0 ⇒ h -3k = 11 …(v)
Solving (iv) and (v), we get
h = 7/2 and k = −5/2
Putting these values of h and k in (ii), we get

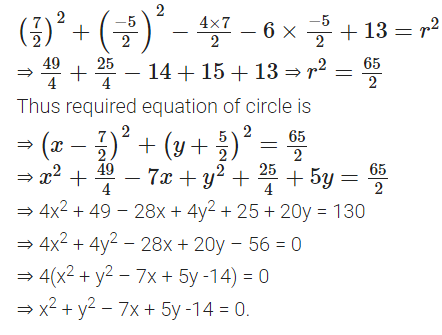
Question 12.
Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2, 3).

Solution:
Since the center of the circle lies on x-axis, the co-ordinates of center are (h, 0). Now the circle passes through the point (2, 3).
∴ Radius of circle

Question 13.
Find the equation of the circle passing through (0, 0) and making intercepts a and b on the co-ordinate axes.

Solution:
Let the circle makes intercepts a with x-axis and b with y-axis.
∴ OA = a and OB = b
So the co-ordinates of A are (a, 0) and B are (0,b)
Now, the circle passes through three points 0(0, 0), A(a, 0) and B(0, b).

Question 14.
Find the equation of a circle with center (2, 2) and passes through the point (4, 5).

Solution:
The equation of circle is
(x – h)² + (y – k)² = r² ….(i)
Since the circle passes through point (4, 5) and co-ordinates of center are (2, 2)
∴ radius of circle

Question 15.
Does the point (-2.5, 3.5) lie inside, outside or on the circle x² + y² = 25?

Solution:
The equation of given circle is x² + y² = 25
⇒ (x – 0)² + (y – 0)² = (5)²
Comparing it with (x – h)² + (y – k)² = r², we
get
h = 0,k = 0, and r = 5
Now, distance of the point (-2.5, 3.5) from the center (0, 0)