Chapter 3 - दो चरों वाले रैखिक समीकरण युग्म (Ex - 3.4)

दो चरों वाले रैखिक समीकरण युग्म

प्रश्न 1.
निम्न समीकरणों के युग्म को विलोपन विधि तथा प्रतिस्थापन विधि से हल कीजिए। कौन-सी विधि अधिक उपयुक्त है?
(i) x + y = 5 और 2x – 3y = 4
(ii) 3x + 4y = 10 और 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 और 9x = 2y + 7
(iv) x2+2y3=−1 और x – y3 = 3
हल
(i) दिया गया रैखिक समीकरण युग्म
x + y = 5 ……. (1)
2x – 3y = 4 …….. (2)
विलोपन विधि : समीकरण (1) को 2 से गुणा करने पर,
2x + 2y = 10 ……. (3)
समीकरण (3) में से समीकरण (2) को घटाने पर,
(2x + 2y) – (2x – 3y) = 10 – 4
2x + 2y – 2x + 3y = 6
5y = 6
y = 65
अब, समीकरण (1) में y = 65 रखने पर,
x + 65 = 5
x = 5−65=25−65=195
अत: समीकरण युग्म का हल x = 195, y = 65
प्रतिस्थापन विधि : समीकरण (1) से,
x + y = 5
⇒ y = (5 – x) …….(4)
y का यह मान समीकरण (2) में रखने पर,
2x – 3(5 – x) = 4
⇒ 2x – 15 + 3x = 4
⇒ 5x = 4 + 15
⇒ 5x = 19
⇒ x = 195
समीकरण (1) में x = 195 रखने पर,
y = 5 – 195
⇒ y = 65
अत: रैखिक समीकरण युग्म का हल x = 195, y = 65
इस प्रश्न को हल करने के लिए विलोपन विधि अधिक उपयुक्त है।

(ii) दिया गया रैखिक समीकरण युग्म
3x + 4y = 10 ……. (1)
2x – 2y = 2 ……. (2)
विलोपन विधि : समीकरण (1) में 2 से गुणा करने पर,
6x + 8y = 20 …….. (3)
समीकरण (2) में 3 से गुणा करने पर,
6x – 6y = 6 ……… (4)
समीकरण (3) में से समीकरण (4) को घटाने पर,
(6x + 8y) – (6x – 6y) = 20 – 6
⇒ 6x + 8y – 6x + 6y = 14
⇒ 14y = 14
⇒ y = 1
समीकरण (1) में y = 1 रखने पर,
3x + 4(1) = 10
⇒ 3x = 10 – 4 = 6
⇒ x = 2
अत: रैखिक समीकरण युग्म का हल x = 2 तथा y = 1
प्रतिस्थापन विधि : समीकरण (2) से,
2x – 2y = 2
⇒ 2x = 2 + 2y
⇒ x = 1 + y
x = 1 + y समीकरण (1) में रखने पर,
3(1 + y) + 4y = 10
3 + 3y + 4y = 10
⇒ 3 + 7y = 10
⇒ 7y = 10 – 3
⇒ 7y = 7
⇒ y = 1
समीकरण (5) में y = 1 रखने पर,
x = 1 + 1 = 2
अत: रैखिक समीकरण युग्म का हल x = 2 तथा y = 1
इस प्रश्न को हल करने के लिए विलोपन विधि अधिक उपयुक्त है।

(iii) दिया गया रैखिक समीकरण युग्म
3x – 5y – 4 = 0 ⇒ 3x – 5y = 4 ……. (1)
9x = 2y + 7 ⇒ 9x – 2y = 7 ……. (2)
विलोपन विधि : समीकरण (1) को 3 से गुणा करने पर,
9x – 15y = 12 ……… (3)
समीकरण (3) में से समीकरण (2) को घटाने पर,
(9x – 15y) – (9x – 2y) = 12 – 7
⇒ 9x – 15y – 9x + 2y = 5
⇒ -13y = 5
⇒ y = −513

अत: रैखिक समीकरण युग्म का हल x = 913 तथा y = −513
इस प्रश्न को हल करने के लिए विलोपन विधि अधिक उपयुक्त है।

(iv) दिया हुआ समीकरण युग्म x2+2y3=−1 और x−y3=3

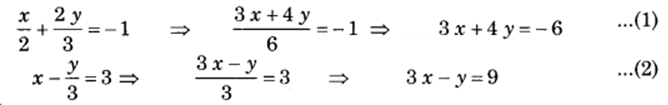
विलोपन विधि : समीकरण (1) में से समीकरण (2) को घटाने पर,
(3x + 4y) – (3x – y) = -6 – 9
⇒ 3x + 4y – 3x + y = -15
⇒ 5y = -15
⇒ y = -3
समीकरण (1) में y = -3 रखने पर,
3x + 4 × (-3) = -6
⇒ 3x – 12 = -6
⇒ 3x = -6 + 12 = 6
⇒ x = 2
अत: रैखिक समीकरण युग्म का हल x = 2 तथा y = -3
प्रतिस्थापन विधि : समीकरण (2) से,
3x – y = 9
⇒ y = 3x – 9
समीकरण (1) में y = 3x – 9 रखने पर,
3x + 4(3x – 9) = -6
⇒ 3x + 12x – 36 = -6
⇒ 15x – 36 = -6
⇒ 15x = -6 + 36 = 30
⇒ x = 2
समीकरण (2) में x = 2 रखने पर,
y = 3 × 2 – 9
⇒ y = 6 – 9
⇒ y = -3
अत: रैखिक समीकरण युग्म का हल x = 2 तथा y = -3
इस प्रश्न को हल करने के लिए विलोपन विधि अधिक उपयुक्त है।

प्रश्न 2.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) विलोपन विधि से ज्ञात कीजिए-
(i) यदि हम अंश में 1जोड़ दें तथा हर में से 1घटा दें, तो भिन्न 1 में बदल जाती है। यदि हर में 1 जोड़ दें, तो यह 12 हो जाती है। वह भिन्न क्या है?
(ii) पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष पश्चात्, नूरी की आयु सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की आयु कितनी है?
(iii) दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना, संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। वह संख्या ज्ञात कीजिए।
(iv) मीना ₹ 2000 निकालने के लिए एक बैंक गई। उसने खजाँची से ₹ 50 तथा ₹ 100 के नोट देने के लिए कहा। मीना ने कुल 25 नोट प्राप्त किए। ज्ञात कीजिए कि उसने ₹ 50 और ₹ 100 के कितने-कितने नोट प्राप्त किए?
(v) किराए पर पुस्तकें देने वाले किसी पुस्तकालय का प्रथम तीन दिनों का एक नियत किराया है तथा उसके बाद प्रत्येक अतिरिक्त दिन का अलग किराया है। सरिता ने सात दिनों तक एक पुस्तक रखने के लिए ₹ 27 अदा किए, जबकि सूसी ने एक पुस्तक पाँच दिनों तक रखने के ₹ 21 अदा किए। नियत किराया तथा प्रत्येक अतिरिक्त दिन का किराया ज्ञात कीजिए।
हल
(i) माना भिन्न का अंश x तथा हर y है, तब भिन्न = xy
यदि भिन्न के अंश में 1 जोड़ा जाए और हर में से 1 घटाया जाए, तो वह हो x+1y−1 जाएगी, परन्तु प्रश्नानुसार वह 1 हो जाएगी।
x+1y−1 = 1
⇒ x + 1 = y – 1
⇒ x = y – 1 – 1
⇒ x = y – 2 …….. (1)
यदि भिन्न के हर में एक जोड़ा जाए, तो वह xy+1 हो जाएगी, परन्तु प्रश्नानुसार 12 हो जाएगी।
xy+1=12
⇒ 2x = y + 1 …….. (2)
समीकरण (1) को 2 से गुणा करके उसमें से समीकरण (2) को घटाने पर,
2(y – 2) – (y + 1) = 0
⇒ 2y – 4 – y – 1 = 0
⇒ 2y – y = +4 + 1
⇒ y = 5
तब, समीकरण (1) से,
x = y – 2 में y = 5 रखने पर,
⇒ x = 5 – 2 = 3
अतः भिन्न (xy)=35

(ii) माना नूरी की वर्तमान आयु x वर्ष तथा सोनू की वर्तमान आयु y वर्ष है।
5 वर्ष पहले नूरी की आयु = (x – 5) वर्ष
5 वर्ष पहले सोनू की आयु = (y – 5) वर्ष
प्रश्नानुसार,
नूरी की आयु = 3 × सोनू की आयु
x – 5 = 3(y – 5)
⇒ x – 5 = 3y – 15
⇒ x = 3y – 15 + 5
⇒ x = 3y – 10 …….. (1)
10 वर्ष पश्चात् नूरी की आयु = (x + 10) वर्ष
10 वर्ष पश्चात् सोनू की आयु = (y + 10) वर्ष
प्रश्नानुसार,
नूरी की आयु = 2 × सोनू की आयु
⇒ x + 10 = 2(y + 10)
⇒ x + 10 = 2y + 20
⇒ x = 2y + 20 – 10
⇒ x = 2y + 10 ….. (2)
समीकरण (1) व समीकरण (2) से,
3y – 10 = 2y + 10
⇒ 3y – 2y = 10 + 10
⇒ y = 20
समीकरण (2) में y = 20 रखने पर,
x = (2 × 20) + 10 = 40 + 10 = 50
अत: नूरी की आयु = 50 वर्ष तथा सोनू की आयु = 20 वर्ष।

(iii) माना संख्या का इकाई का अंक x तथा दहाई का अंक y है।
संख्या = 10y + x
संख्या के अंकों का योग = 9
इकाई का अंक + दहाई का अंक = 9
x + y = 9
मूल संख्या 10y + x है, तब अंकों के पलटने पर प्राप्त संख्या = 10x + y
प्रश्नानुसार,
संख्या का 9 गुना = अंकों के पलटने से प्राप्त संख्या का दो गुना
(10y + x) × 9 = (10x + y) × 2
⇒ 9x + 90y = 20x + 2y
⇒ 90y – 2y = 20x – 9x
⇒ 88y = 11x
⇒ 8y = x (दोनों पक्षों में सार्व 11 का भाग देने पर)
⇒ x = 8y ……. (2)
समीकरण (2) से x का मान समीकरण (1) में रखने पर,
8y + y = 9 या 9y = 9 या y = 1
तब, समीकरण (2) में, y = 1 रखने पर,
x = 8 × y = 8 × 1 = 8
संख्या 10y + x = (10 × 1) + 8 = 10 + 8 = 18
अतः संख्या = 18

(iv) माना ₹ 50 मूल्य वाले नोटों की संख्या : तथा ₹ 100 मूल्य वाले नोटों की संख्या y थी।
कुल नोटों की संख्या = (x + y)
परन्तु प्रश्नानुसार नोटों की कुल संख्या 25 थी।
x + y = 25 …….. (1)
₹ 50 वाले x नोट थे, उनका मूल्य = ₹ 50x
₹ 100 वाले के नोट थे, उनका मूल्य = ₹ 100y
कुल नोटों का मूल्य = (50x + 100y) = ₹ 50(x + 2y)
प्रश्नानुसार, मीना ने केवल ₹ 2000 बैंक से निकाले।
50(x + 2y) = 2000
⇒ x + 2y = 40 …….. (2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(x + 2y) – (x + y) = 40 – 25
⇒ x + 2y – x – y = 15
⇒ y = 15
समीकरण (1) में y = 15 रखने पर,
x + 15 = 25
⇒ x = 10
अतः मीना ने ₹ 50 मूल्य वाले 10 नोट तथा ₹ 100 मूल्य वाले 15 नोट प्राप्त किए।

(v) माना प्रथम तीन दिनों तक के लिए पुस्तकालय का नियत किराया ₹ x है तथा उसके बाद प्रत्येक अतिरिक्त दिन का किराया ₹ y है।
7 दिनों में एक पुस्तक का किराया = प्रथम 3 दिन का नियत किराया + 4 अतिरिक्त दिन का किराया
= ₹ x + ₹ 4 × y
= ₹(x + 4y)
परन्तु सरिता ने 7 दिन का किराया ₹ 27 अदा किया।
x + 4y = 27 …….(1)
5 दिनों में एक पुस्तक का किराया = प्रथम 3 दिन का नियत किराया + 2 अतिरिक्त दिन का किराया
= ₹ x + ₹ 2y
= ₹(x + 2y)
परन्तु सूसी ने 5 दिन का किराया ₹ 21 अदा किया।
x + 2y = 21 ……… (2)
समीकरण (1) में से समीकरण (2) को घटाने पर,
(x + 4y) – (x + 2y) = 27 – 21
⇒ x + 4y – x – 2y = 6
⇒ 2y = 6
⇒ y = 3
समीकरण (2) में y = 3 रखने पर,
x + (2 × 3) = 21
⇒ x + 6 = 21
⇒ x = 21 – 6 = 15
अतः पुस्तकालय की किसी पुस्तक का प्रथम 3 दिन तक का नियत किराया ₹ 15 है तथा उसके बाद प्रत्येक अतिरिक्त दिन का किराया ₹3 है।