Chapter 5 – द्रव्य की अवस्थाएँ

द्रव्य की अवस्थाएँ 

अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 5.1
30°C तथा 1 bar दाब पर वायु के 500 dm³ आयतन को 200 dm³ तक संपीडित करने के लिए कितने न्यूनतम दाब की आवश्यकता होगी?

उत्तर:
प्रश्नानुसार,
P₁ = 1 bar
P₂ = ?
V₁ = 500 dm
V₂ = 200 dm³
∵ ताप स्थिर है;
∴ बॉयल के नियम से
P₁V₁ = P₂V₂
या P₂ = P₁V₁/V₂
P₂ = (1bar)×(50dm³)/(20dm³)
= 2.5 bar

प्रश्न 5.2
35°C ताप तथा 1.2 bar दाब पर 120 mL धारिता वाले पात्र में गैस की निश्चित मात्रा भरी है। यदि 35°C पर गैस को 180 mL धारिता वाले फ्लास्क में स्थानान्तरित किया जाता है तो गैस का क्या दाब होगा?

उत्तर:
प्रश्नानुसार,
P₁ = 1.2 bar P₂ = ?
V₁ = 120mL V₂ = 180mL
∵ ताप स्थिर है
∴ बॉयल के नियम से
P₁V₁ = P₂V₂
या P₂ = (1.2bar)×(120mL)/(180mL)
= 0.8 bar

प्रश्न 5.3
अवस्था-समीकरण का उपयोग करते हुए स्पष्ट कीजिए कि दिये गये ताप पर गैस का घनत्व गैस के दाब के समानुपाती होता है।

उत्तर:
गैस समीकरण PV = nRT से
P = nRT/V …………. (i)

समीकरण (ii) से n का मान (i) में रखने पर
P = mRT/MV ………….. (iii)
हम जानते हैं कि घनत्व (d) = m/V
या P = dRT/M
या d ∝ P
अत: दिये हुए ताप पर गैस का घनत्व गैस दाब के समानुपाती होता है।

प्रश्न 5.4
0°C पर तथा 2 bar दाब पर किसी गैस के ऑक्साइड का घनत्व 5 bar दाब पर डाइनाइट्रोजन के घनत्व के समान है तो ऑक्साइड का अणु-भार क्या है?

उत्तर:
गैस का घनत्वं (d) = PM/RT
यहाँ गैसों के लिए R तथा T स्थिरांक हैं।
नाइट्रोजन के लिए, P = 5bar, M = 28g mol^-1
∴ d_N2 = PM/RT
= (5bar)×(28gmol−1)/(R×T)
गैसीय ऑक्साइड के लिए, P = 2 bar; M = ?

प्रश्नानुसार,

प्रश्न 5.5
27°C पर 1g आदर्श गैस का दाब 2 bar है। जब समान ताप एवं दाब पर इसमें 2g आदर्श गैस मिलाई जाती है तो दाब 3 bar हो जाता है। इन गैसों के अणु-भार में सम्बन्ध स्थापित कीजिए।

उत्तर:
माना दोनों गैसों A तथा B के मोलर द्रव्यमान क्रमश: M_A तथा M_B हैं। दिए गए आँकड़ों के अनुसार,

अब,
गैस A का दाब (P_A) = 2 bar
गैस A तथा B का दाब (P_A + P_B) = 3bar
P_B = (3 – 2) = 1bar
आदर्श गेस समीकरण के अनुसार,
P_AV = n_A RT
P_BV = n_B RT
∴ P_A/P_B=n_A/n_B
या n_A/n_B = (2bar)/(1bar) = 2/1 …………… (ii)
समीकरण (i) तथा (ii) से,
M_B/2M_A = 2/1 या M_B = 4ML_A

प्रश्न 5.6
नाली साफ करने वाले ड्रेनेक्स में सूक्ष्म मात्रा में एल्यूमीनियम होता है। यह कॉस्टिक सोडा से क्रिया पर डाइहाड्रोजन गैस देता है। यदि 1 bar तथा 20°C ताप पर 0.15g एल्यूमीनियम अभिक्रिया करेगा तो निर्गमित डाइहाइड्रोजन का आयतन क्या होगा?

उत्तर:
अभिक्रिया का रासायनिक समीकरण निम्नलिखित

प्रश्न 5.7
यदि 27°C पर 9dm³ धारिता वाले फ्लास्क में 3.2g मेथेन तथा 4.4g कार्बन डाइ-ऑक्साइड का मिश्रण हो तो इसका दाब क्या होगा?

उत्तर:
मेथेन (CH₄) के मोलों की संख्या

= 0.2mol

कार्बन डाइ-ऑक्साइड (CO₂) के मोलों की संख्या

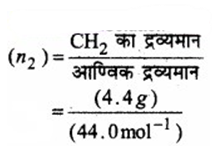
= 0.1mol
_pCH₄ = n₁RT/V

अतः गैसीय मिश्रण का कुल दाब
(P) = _pCH₄ + _pCO₄
= (5.543 × 10⁴ Pa) + (2.771 × 10⁴Pa)
= 8.314 × 10⁴ Pa

प्रश्न 5.8
27°C ताप पर जब 1L के फ्लास्क में 0.7 bar पर 2.0 L डाइऑक्सीजन तथा 0.8 bar पर 0.5L डाइहाइड्रोजन को भरा जाता है तो गैसीय मिश्रण का दाब क्या होगा?

उत्तर:
डाइऑक्सीजन (O₂) के लिए,

गैस समीकरण के अनुसार,
PV = nRT
या P = nRT/V = (1.8barL/RT) × RT/(L)
= 1.8 bar

प्रश्न 5.9
यदि 27°C ताप तथा 2 bar दाब पर एक गैस का घनत्व 5.46g/dm³ तो STP पर इसका घनत्व क्या होगा?

उत्तर:

प्रश्न 5.10
यदि 546°C तथा 0.1 bar दाब पर 34.05 mL फॉस्फोरस वाष्प का भार 0.0625 g है तो फॉस्फोरस का मोलर द्रव्यमान क्या होगा?

उत्तर:
आदर्श गैस समीकरण के अनुसार,
PV = nRT
या PV = WRT/M
या M = WRT/PV
दिए गए आँकड़े-
फॉस्फोरस वाष्पों का द्रव्यमान (W) = 0.0625g
वाष्पों का आयतन (V) = 34.05 mL = 34.05 × 10^-3L
वाष्पों का दाब (P) = 0.1bar
गैस स्थिरांक (R) = 0.083 bar LK^-1 mol^-1
ताप (T) = 546 + 273 = 819K
उपर्युक्त समीकरण में मान रखने पर,

प्रश्न 5.11
एक विद्यार्थी 27°C पर गोल पेंदे के फ्लास्क में अभिक्रिया-मिश्रण डालना भूल गया तथा उस फ्लास्क को ज्वाला पर रख दिया। कुछ समय पश्चात् उसे अपनी भूल का अहसास हुआ। उसने उत्तापमापी की सहायता से फ्लास्क का ताप 477°C पाया। आप बताइए कि वायु का कितना भाग फ्लास्क से बाहर निकला?

उत्तर:
चूँकि विद्यार्थी प्रयोगशाला में कार्य कर रहा था, इसलिए दाब में कोई परिवर्तन नहीं है। अतः चार्ल्स का नियम लागू होगा।
दिए गए आंकड़े हैं –
V₁ = V_L (माना) V₂ = ?
T₁ = 27 + 273 = 300K
T₂ = 477 + 273 = 750K
∴ V₂=V₁T₂/T₁
= {(VL)×(750K)}/(300K) = 2.5V
अतः बाहर निकलने वाली वायु का आयतन
= 2.5V – V = 1.5V
बाहर निकलने वाली वायु का भाग = 1.5V/2.5V = 35

प्रश्न 5.12
3.32 bar पर 5 dm³ आयतन घेरने वाली 4.0 mol गैस के ताप की गणना कीजिए। (R = 0.83 bar dm³ K^-1 mol^-1)

उत्तर:
प्रश्नानुसार, गैस के मोलों की संख्या (n)= 4.0 मोल
गैस का दाब (P) = 3.32bar, गैस का आयतन (V) = 5dm³ तथा R = 0.083 bar dm³ K^-1 mol^-1
अब गैस समीकरण
PV = nRT से
T = PV/nR
= 3.32bar×5dm³/4.0mol×0.083bardm³K⁻¹mol⁻¹
= 50K

प्रश्न 5.13
1.4g डाइ-नाइट्रोजन गैस में उपस्थित कुल इलेक्ट्रॉनों की संख्या की गणना कीजिए।

उत्तर:
डाइनाइट्रोजन (N₂) का आणविक द्रव्यमान = 28g
∵ 28g N₂ में अणुओं की संख्या = 6.022 × 10²³
∴ 1.4g N₂ में अणुओं की संख्या
= 6.022×10²³×1.4g/28g
= 3.0 × 10²²
∵ N₂ का परमाणु क्रमांक = 7
∴ N₂ के एक अणु में इलेक्ट्रॉनों की संख्या
= 2 × 7 = 14
अत: N₂ के 3.011 × 10²² अणुओं में इलेक्ट्रॉनों की संख्या = 14 × 3.011 × 10²²
= 4.215 × 10²²

प्रश्न 5.14
यदि एक सेकण्ड में 10 × 10¹⁰ गेहूँ के दाने वितरित किये जायें तो आवोगाद्रो-संख्या के बराबर दाने वितरित करने में कितना समय लगेगा?

उत्तर:
∵ 10^1o दानों का वितरित करने में लगा समय = 1s
∴ 6.022 × 10²² दानों को वितरित करने में समय लगेगा

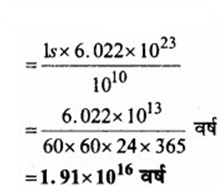
प्रश्न 5.15
27°C ताप पर 1dm³ आयतन वाले फ्लास्क में 8g डाइ-ऑक्सीजन तथा 4g डाइ-हाइड्रोजन के मिश्रण का कुल दाब कितना होगा?

उत्तर:
डाइ-ऑक्सीजन (O₂) के मोलों की संख्या = (n₁)

अतः गैसीय मिश्रण का कुल दाब = PO₂ + PH₂
= 6.225 + 49.8
= 56.025 bar

प्रश्न 5.16
गुब्बारे के भार तथा विस्थापित वायु के भार के अन्तर को ‘पेलोड’ कहते हैं। यदि 27°C पर 10 m त्रिज्या वाले गुब्बारे में 1.66 bar पर 100 kg हीलियम भरी जाये तो पेलोड की गणना कीजिए। (वायु का घनत्व = 1.2 kg m^-3 तथा R = 0.083 bar dm³ K^-1 mol^-1)

उत्तर:
∵ गुब्बारे की त्रिज्या (Ω) = 10m
∴ गुब्बारे का आयतन = 4/3 πΩ³
= 4/3 × 22/7 × (10m)³
= 4190.5m³
तथा विस्थापित वायु का द्रव्यमान
= वायु का आयतन × वायु का घनत्व
= 4190.5m³ × 1.2kg m^-3
= 5028.6kg
पुनः चूंकि
P = 1.66bar, V = 4190.5 × 10³ dm³
R = 0.083 bardm³ K^-1 mol^-1
T = 27 + 273 = 300 K
आदर्श गैस समीकरण
PV = nRT से
हीलियम (He) के मोलों की संख्या (n) = PV/RT
=(1.66bar×4190×10³dm³)/(0.083bardm³K⁻¹mol⁻¹×300K)
= 1117.48 × 10³g = 1117.48kg
तथा भरे हुए गुब्बारे का द्रव्यमान
= 100 + 1117.48
= 1217.48kg
He का द्रव्यमान = He के मोल × मोलर द्रव्यमान
= 279.37 × 10 mol × 4g mol^-1
= 1117.48 × 10³ × 4gmol^-1
= 1117.48 × 10³g = 1217.48kg
अतः पेलोड = विस्थापित वायु का द्रव्यामान – भरे हुए गुब्बारे का द्रव्यमान
= 5028.6 – 1217.48
= 3811.12 kg

प्रश्न 5.17
31.1°C और 1 bar दाब पर 8.8 ग्राम CO₂, द्वारा घेरे गये आयतन की गणना कीजिए। (R = 0.083 bar LK^-1 mol^-1)

उत्तर:
प्रश्नानुसार
CO₂ का दाब (P) = 1bar, ताप (T) = 273 + 31.1
= 304.1°K तथा R = 0.083 bar Lmol^-1

= (8.8g)/(44gmol−1)
= 0.2 mol
अब गैस समीकरण से
PV = nRT
V = nRT/p

= 5.048L

प्रश्न 5.18
समान दाब पर किसी गैस के 2.9g द्रव्यमान का 95°C तथा 0.184g डाइहाइड्रोजन का 17°C पर आयतन समान है। बताइए कि गैस का मोलर द्रव्यमान क्या होगा?

उत्तर:
माना गैस का मोलर द्रव्यमान M है तो

= 2.9gM
तथा डाइहाइड्रोजन (H₂) के मोलों की संख्या

गैस का ताप (T₂) = 95 + 273 = 368°K
तथा H₂ का ताप (T₂) = 17 + 273 = 290°K
आदर्श गैस समीकरण से,
PV = nRT
∵ दोनों गैसों के लिए P, V तथा R स्थिरांक हैं।

प्रश्न 5.19
1 bar दाब पर डाइहाइड्रोजन तथा डाइऑक्सीजन के मिश्रण में 20% डाइहाइड्रोजन (भार से) रखा जाता है तो डाइहाइड्रोजन का आंशिक दाब क्या होगा?

उत्तर:
यदि मिश्रण में H₂ का द्रव्यमान 20g हो तो O₂ का द्रव्यमान 80g होगा।
मिश्रण में H₂ के मोलों की संख्या

∵ गैसीय मिश्रण का कुल दाब (P) = 1bar
अतः डाइहाइड्रोजन (H₂) का आंशिक दाब

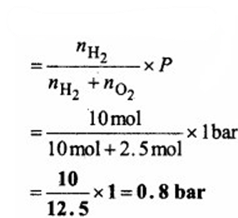
प्रश्न 5.20
pV²T²/n राशि के लिए S. I इकाई क्या होगी?

उत्तर:

प्रश्न 5.21
चार्ल्स के नियम के आधार पर समझाइए कि न्यूनतम सम्भव ताप – 273°C होता है।

उत्तर:
273°C (या OK) ताप, परम शून्य ताप कहलाता है। इस ताप से नीचे कोई पदार्थ गैस अवस्था में नहीं रह सकता तथा यह द्रव अवस्था प्राप्त कर लेता है। इसका तात्पर्य यह है कि चार्ल्स का नियम केवल -273°C ताप तक ही लागू किया जा सकता है, चूंकि इस ताप से नीचे पदार्थ गैस अवस्था में नहीं होता अर्थात् न्यूनतम सम्भव ताप -273°C होता है।

प्रश्न 5.22
कार्बन डाइऑक्साइड तथा मेथेन का क्रान्तिक ताप क्रमशः 31.1°C एवं – 81.9°C है। इनमें से किसमें प्रबल अन्तर-आण्विक बल है तथा क्यों?

उत्तर:
क्रान्तिक तापों के दिए गए मान यह दर्शाते हैं कि कार्बन डाइऑक्साइड के अणुओं में आकर्षण बल अधिक है। वास्तव में दोनों गैसें अध्रुवी हैं, परन्तु कार्बन डाइऑक्साइड के अणुओं में वाण्डरवाल्स आकर्षण बल अधिक होता है; क्योंकि इसका आण्विक आकार बड़ा है।

प्रश्न 5.23
वाण्डरवाल्स प्राचल की भौतिक सार्थकता को समझाइए।

उत्तर:
1. वाण्डरवाल्स प्राचल ‘a’:
इसका मान गैस के अणुओं में विद्यमान आकर्षण बलों के परिमाण की माप होता है। अत: a का मान अधिक होने का तात्पर्य, अन्तर-आण्विक – आकर्षण बलों का अधिक होना है।

2. वाण्डरवाल्स प्राचल ‘b’:
इसका मान गैस-अणुओं के प्रभावी आकार की माप है। इसका मान गैस-अणुओं के वास्तविक आयतन का चार गुना होता है। यह अपवर्जित आयतन कहलाता है।