Introduction to Three Dimensional Geometry (Ex – 12.2)
Question 1.
Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1)
(ii) (-3, 7, 2) and (2, 4, -1)
(iii) (-1, 3, -4) and (1, -3, 4)
(iv) (2, -1, 3) and (-2, 1, 3)
Solution:
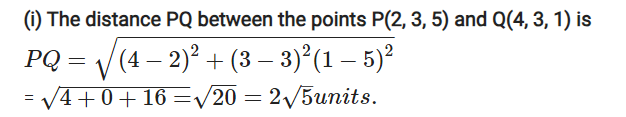

Question 2.
Show that the points (-2, 3, 5), (1, 2, 3) and (7, 0, -1) are collinear.
Solution:
Let A(-2, 3, 5), B(1, 2, 3) and C(7, 0, -1) be three given points.

Now AC = AB + BC
Thus, points A, B and C are collinear.
Question 3.
Verify the following:
(i) (0, 7, -10), (1, 6, -6) and (4, 9, -6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (-1, 6, 6) and (-4, 9, 6) are the vertices of a right angled triangle.
(iii) (-1, 2, 1), (1, -2, 5), (4, -7,8) and (2, -3,4) are the vertices of a parallelogram.
Solution:
(i) Let A(0, 7, -10), B(l, 6, -6) and C(4, 9, -6) be three vertices of triangle ABC. Then

Now, AB = BC
Thus, ABC is an isosceles triangle.
(ii) Let A(0, 7,10), B(-l, 6, 6) and C(-A, 9, 6) be three vertices of triangle ABC. Then

Now, AC2 = AB2 + BC2
Thus, ABC is a right angled triangle.
(iii) Let A(-1, 2, 1), B(1, -2, 5) and C(4, -7, 8) and D(2, -3,4) be four vertices of quadrilateral ABCD. Then

Now AB = CD, BC = AD and AC ≠ BD
Thus A, B, C and D are vertices of a parallelogram ABCD.
Question 4.
Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, -1).
Solution:
Let A(x, y, z) be any point which is equidistant from points B(1, 2, 3) and C(3, 2, -1).

Question 5.
Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(-4,0,0) is equal to 10.
Solution:
Let P(x, y, z) be any point.


