Permutations and Combinations (Ex – 7.4)
Question 1.
If nC8 = nC2, find nC2.
Solution.
We have, nC8 = nC2

Question 2.
Determine n if
(i) 2nC3: nC3 =12 : 1
(ii) 2nC3: nC3= 11 : 1
Solution.

Question 3.
How many chords can be drawn through 21 points on a circle?
Solution.
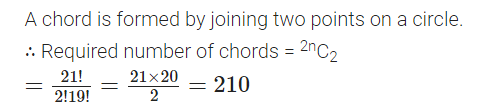
Question 4.
In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
Solution.

Question 5.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each color.
Solution.
No. of ways of selecting 3 red balls =6C3
No. of ways of selecting 3 white balls = 5C3
No. of ways of selecting 3 blue balls = 5C3
∴ Required no. of ways of selecting 9 balls

Question 6.
Determine the number of 5 cards combinations out of a deck of 52 cards if there is exactly one ace in each combination.
Solution.
Total no. of cards = 52
No. of ace cards = 4
No. of non-ace cards = 48
∴ One ace card out of 4 can be selected in 4C1 ways.
Remaining 4 cards out of 48 cards can be selected in 48C4ways.
∴ Required no. of ways of selecting 5 cards

Question 7.
In Kbw many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
Solution.
Total players = 17, No. of bowlers = 5,
No. of non-bowlers = 12
No. of ways of selecting 4 bowlers = 5C4
No. of ways of selecting 7 non-bowlers = 12C7
∴ Required no. of ways of selecting a cricket team

Question 8.
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
Solution.
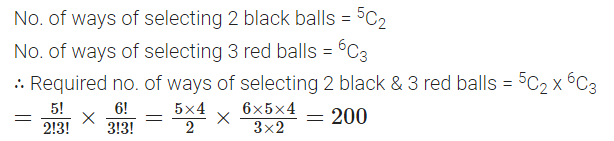
Question 9.
In how many ways can a student choose a program of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
Solution.

