Chapter 2 – Polynomials (Ex – 2.2)

Polynomials

Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:

1. x² – 2x – 8
2. 4s² – 4s + 1
3. 6x² – 3 – 7x
4. 4u² + 8u
5. t² – 15
6. 3x² – x – 4

Solution:
1. We have:
x² – 2x – 8
= x² + 2 – 4x – 8
= x(x + 2) – 4(x + 2)
= (x + 2)(x – 4)
The value of x² – 2x – 8 is 0, when the value of (x + 2)(x – 4) is 0, i.e., when x + 2 = 0 or x – 4 = 0, i.e., when x = – 2 or x = 4.
∴ The zeroes of x² – 2x – 8 are – 2 and 4.
Therefore, sum of the zeroes = (- 2) + 4
= 2
= −(−2)/1

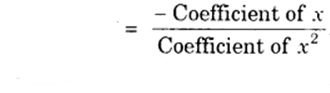
and product of zeroes = (- 2)(4)
= – 8
= −8/1

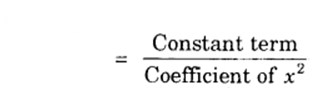
2. We have:
4s² – 4s + 1
= 4s² – 2s – 2s + 1
= 2s(2s – 1) – 1(2s – 1)
= (2s – 1)(2s – 1)
The value of 4s² – 4s + 1 is 0, when the value of (2s – 1)(2s – 1) is 0, i.e., when 2s – 1 = 0 or 2s – 1 = 0, i.e.,
when s = 12 or s = 12.
∴ The zeroes of 4s² – 4s + 1 are 1/2 and 1/2.
Therefore, sum of the zeroes = 1/2 + 1/2 
= 1
= −(−4)/4

3. We have:
6x² – 3 – 7x
= 6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (3x + 1)(2x – 3)
The value of 6x² – 3 – 7x is 0, when the value of (3x + 1)(2x – 3) is 0, i.e; when 3x + 1 = 0 or 2x – 3 = 0, i.e;
when x = – 1/3 or x = 3/2.
∴ The zeros of 6x² – 3 – 7x are – 1/3 and 3/2.
Therefore, sum of the zeros = – 1/3 + 3/2 
= 7/6 
= −(−7)/6

4. We have:
4u² + 8u is 0, when the value of 4u(u + 2) is 0, i.e; when u = 0 or u + 2 = 0, i.e; when u = 0 or u = – 2.
∴ The zeroes of 4u² + 8u are o and – 2.
Therefore, sum of the zeroes = 0 + (- 2)
= – 2
= −8/4

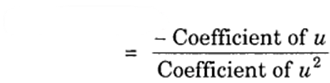
and product of zeroes = (0)(- 2)
= 0
= 0/4

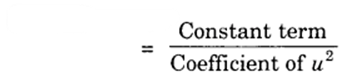
5. We have:
t – 15 = (t – √15)(t + √15)
The value of t² – 15 is 0, when the value of (t – √15)(t + √15) is 0, i.e; when t – √15 = 0 or t + √15 = 0,
i.e; when t = √15 or t = – √15.
∴ The zeroes of t² – 15 are √15 and – √15.
Therefore, sum of the zeroes = √15 + (- √15) = 0

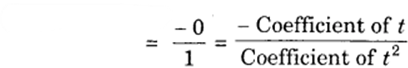
and product of the zeroes = (√15)(-√15)
= – 15
= −15/1

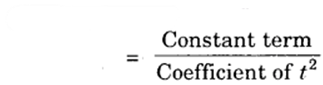
6. We have:
3x² – x – 4
= 3x² + 3x – 4x – 4
= 3x(x + 1) – 4(x + 1)
= (x + 1)(3x – 4)
The value of 3x² – x – 4 is 0, when the value of (x + 1)(3x – 4) is 0, i.e; when x + 1 = 0 or 3x – 4 = 0, i,e; when x = – 1 or x = 4/3.
∴ The zeroes of 3x² – x – 4 are – 1 and 4/3.
Therefore, sum of the zeroes = – 1 + 4/3 = (−3+4)/3
= 1/3 
= −(−1)/3

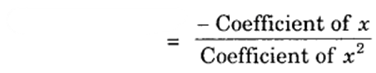
and product of the zeroes = (- 1)(4/3)
= – 4/3 
= −4/3

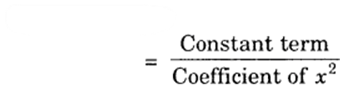
Question 2.
Find a quadratie polynomial each with the given numbers as the sum and product of its zeroes respectively.

1. 1/4, – 1
2. √2, 1/3
3. 0, √5
4. 1, 1
5. – 1/4, 1/4
6. 4, 1

Solution:
1. Let the polynomial be ax² + bx + c, and its zeroes be α and β. Then,

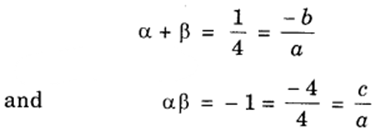
If a = 4, then b = – 1 and c = – 4.
∴ One quadratic polynomial which fits the given conditions is 4x² – x – 4.

2. Let the polynomial be ax² + bx + c, and its zeroes be α and β. Then,

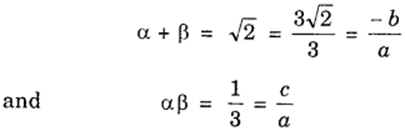
If a = 3, then b = – 3√2 and c = 1.
∴ One quadratic polynomial which fits the given conditions is 3x² – 3√2x + 1.

3. Let the polynomial be ax² + bx + c, and its zeroes be α and β. Then,

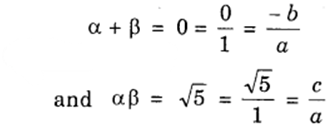
If a = 1, then b = 0 and c = √5.
∴ One quadratic polynomial which fits the given conditions is x² – 0. x + √5, i.e; x² + √5.

4. Let the polynomial be ax² + bx + c, and its zeroes be α and β. Then,

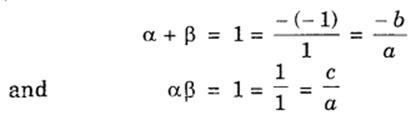
If a = 1, then b = – 1 and c = 1.
∴ One quadratic polynomial which fits the given conditions is x² – x + 1.

5. Let the polynomial be ax² + bx + c and its zeroes be α and β. Then

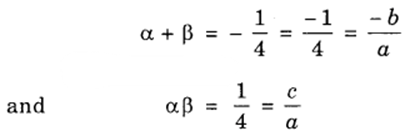
If a = 4, then b = 1 and c = 1.
∴ One quadratic polynomial which fits the given conditions is 4x² + x + 1.

6. Let the polynomial be ax² + bx + c and its zeroes be α and β. Then,

If a = 1, then b = – 4, and c = 1.
∴ One quadratic polynomial which fits the given conditions is x² – 4x + 1.