Chapter 2 – Polynomials (Ex – 2.4)

Polynomials

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeros.
Also verify the relationship between the zeroes and the coefficients in each case:

1. 2x³ + x² – 5x + 2; 1/2, 1, – 2
2. x³ – 4x² + 5x – 2; 2, 1, 1

Solution:
1. Comparing the given polynomial with ax³ + bx² + cx + d, we get
a = 2, b = 1, c = – 5 and d = 2.

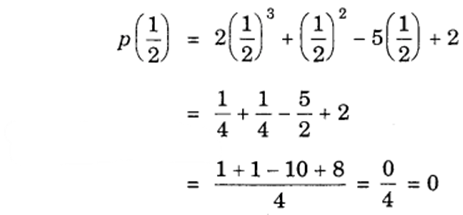
p(1) = 2(1)³ + (1)² – 5(1) + 2
= 2 + 1 – 5 + 2 = 0
p(- 2) = 2(- 2)³ + (- 2)² – 5(- 2) + 2
= 2(- 8) + 4 + 10 + 2
= – 16 + 16 = 0
∴ 1/2, 1 and – 2 are the zeroes of 2x³ + x² – 5x + 2.
So, α = 1/2, β = 1 and γ = – 2.

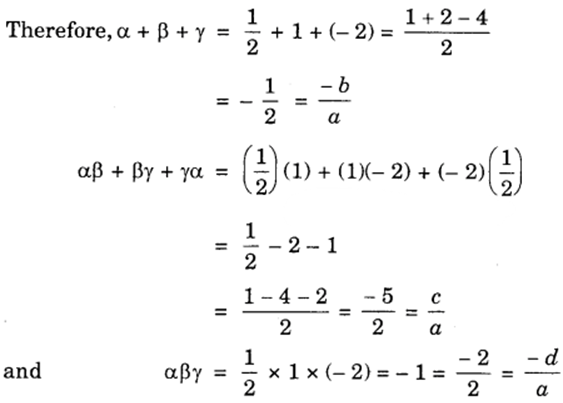
2. Comparing the given polynomial with ax³ + bx² + cx + d, we get
a = 1, b = – 4, c = 5 and d = – 2.
p(2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 16 + 10 – 2
= 0
p(1) = (1)³ – 4(1)² + 5(1) – 2
= 1 – 4 + 5 – 2
= 0
∴ 2, 1 and 1 are the zeroes of x³ – 4x² + 5x – 2.
So, α = 2, β = 1 and γ = 1.
Therefore, α + β + γ
= 2 + 1 + 1
= 4
= −(−4)/1 
= −b/a
αβ + βγ + γα
= (2)(1) + (1)(1) + (1)(2)
= 2 + 1 + 2 + 5
= 5/1 
= c/a
and αβγ
= (2)(1)(1)
= 2
= −(−2)/1 
= −d/a.

Question 2.
Find a cubic polynomial with the sum, sum of the products of its zeroes taken two at a time, and the product of its zeroes as 2, – 7, – 14 respectively.

Solution:
Let the cubic polynomial be ax³ + bx² + cx + d, and its zeroes be α, β and γ.
Then, α + β + γ = 2 = −(−2)/1 = −b/a
αβ + βγ + γα = – 7 = −7/1 = c/a
and αβγ = – 14 = −14/1 = −d/a
If a = 1, then b = – 2, c = – 7 and d = 14.
So, one cubic polynomial which fits the given conditions x³ – 2x² – 7x + 14.

Question 3.
If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a and a + b, find a and b.

Solution:
Since (a – b), a and (a + b) are the zeroes of the polynomial x³ – 3x² + x + 1, therefore
So, (a – b) + a + (a + b) = −(−3)/1 = 3
So, 3a = 3 or a = 1
(a – b)a + a(a + b) + (a + b)(a – b) = 1/1 = 1
or a² – ab + a² + ab + a² – b² = 1
or 3a² – b² = 1
So, 3(1)² – b² = 1 [∵ a = 1]
or 3 – b² = 1
or b² = 2
or b = ± √2
Hence, a = 1 and b = ± √2.

Question 4.
If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2 ± √3, find other zeroes.

Solution:
We have:
2 ± √3 are two zeroes of the polynomial p(x) = x⁴ – 6x³ – 26x² + 138x – 35
Let x = 2 ± √3. So, x – 2 = ± √3
Squaring, we get
x² – 4x + 4 = 3, i.e; x² – 4x + 1 = 0
Let us divide p(x) by x² – 4x + 1 to obtain other zeroes.

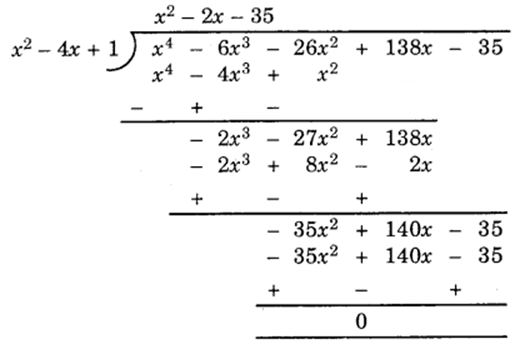
∴ p(x) = x⁴ – 6x³ – 26x² + 138x – 35
= (x² – 4x + 1)(x² – 2x – 35)
= (x² – 4x + 1)(x² – 7x + 5x – 35)
= (x² – 4x + 1)[x(x – 7) + 5(x – 7)]
= (x² – 4x + 1)(x + 5)(x – 7)
So, (x + 5) and (x – 7) are other factors of p(x).
∴ – 5 and 7 are other zeroes of the given polynomial.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.

Solution:
Let us divide x⁴ – 6x³ + 16x² – 25x + 10 by x² – 2x + k.

∴ Remainder = (2k – 9)x – (8 – k)k + 10
But the remainder is given as x + a.
On comparing their coefficients, we have:
2k – 9 = 1 or 2k = 10 or k = 5
and – (8 – k)k + 10 = a
So, a = – (8 – 5)5 + 10
= – 3 × 5 + 10 = – 15 + 10 = – 5
Hence, k = 5 and a = – 5.