Chapter 11 - रचनाएँ (Ex - 11.1)

रचनाएँ

निम्नलिखित में से प्रत्येक के लिए रचना का औचित्य भी दीजिए।

प्रश्न 1.
7.6 cm लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल
दिया है : रेखाखण्ड AB = 7.6 cm
रचना करनी है : रेखा AB को 5 : 8 में विभाजित करने की।
रचना विधि :
1. रेखाखण्ड AB = 7.6 cm खींचा।
2. रेखाखण्ड AB पर बिन्दु A से न्यूनकोण बनाती हुई एक ऋजु रेखा AX खींची।

3. रेखा AX में से समान लम्बाई के (5 + 8 = 13) भाग AA₁, A₁A₂, A₂A₃, A₃A₄, A₄A₅, A₅A₆, A₆A₇, A₇A₈, A₈A₉, A₉A₁₀, A₁₀A₁₁, A₁₁A₁₂ व A₁₂A₁₃ खण्ड काटे।
4. रेखाखण्ड AB खींचा।
5. बिन्दु A₅ से A₁₃B के समान्तर रेखा A₅P खींची जो AB को बिन्दु P पर काटती है।
AP तथा PB, रेखाखण्ड AB के अभीष्ट भाग हैं जो 5 : 8 के अनुपात में हैं।
औचित्य ( उपपत्ति) :
∆AA₅P तथा ∆AA₁₃B में A₅P || A₁₃B
अतः ये त्रिभुज परस्पर समरूप हैं।
∴ AA₅ : A₅A₁₃ = AP : PB
परन्तु AA₅ : A₅A₁₃ = 5 : 8
∴ AP : PB = 5 : 8
मापने पर : AP = 2.9 cm व PB = 4.7 cm

प्रश्न 2.
4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 23 गुनी हों।
हल
दिया है : ∆ABC में भुजा AB = 4.0 cm, BC = 5.0 cm तथा CA = 6.0 cm
रचना करनी है : ∆ABC के समरूप एक ∆A’BC’ की जिसकी प्रत्येक भुजा ∆ABC की संगत भुजा की 23 हो।
रचना विधि :
1. ऋजु रेखा BC = 5.0 cm खींची।
2. B को केन्द्र मानकर 4.0 cm त्रिज्या से और C को केन्द्र मानकर 6.0 cm त्रिज्या से चाप लगाए जो परस्पर A पर काटते हैं।

3. ऋजु रेखाओं AB तथा AC को पूरा किया।
4. B से एक ऋजु रेखा BD खींचकर उसमें से BB₁, BB₂, BB₃ तीन समान भाग काटे।
5. ऋजु रेखा CB₃ खींची।
6. B₂ से CB₃ के समान्तर ऋजु रेखा C’B₂ खींची जिससे
BC’ = 23 BC
7. C’ से CA के समान्तर ऋजु रेखा C’A’ खींची जो AB को A’ पर मिलती है जिससे
A’B = 23 AB
∆A’BC’अभीष्ट समरूप त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 2 : 3
BC’ : BC = 2 : 3
⇒ BC’ = 23 BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 2 : 3
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की 23 हैं।
इति सिद्धम्

प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 75 गुनी हों।
हल
दिया है : 5 cm, 6 cm, 7 cm भुजाओं वाला एक त्रिभुज।
रचना करनी है : उपर्युक्त त्रिभुज के समरूप एक अन्य त्रिभुज की जिसकी प्रत्येक भुजा दिए त्रिभुज की प्रत्येक संगत भुजा का 75 वाँ भाग हो।
रचना विधि :
1. रेखाखण्ड BC = 6 cm खींचा।
2. B को केन्द्र मानकर 5 cm त्रिज्या से एवं C को केन्द्र मानकर 7 cm त्रिज्या के चाप खींचे जो परस्पर A पर काटते हैं।
3. रेखाखण्ड AB तथा AC खींचकर दिया हुआ त्रिभुज ABC प्राप्त किया।
4. बिन्दु B से रेखा BD खींची और उसमें से BB₁, B₁B₂, B₂B₃, B₃B₄, B₄B₅, B₅B₆ तथा B₆B₇ सात समान भाग काटे।

5. रेखाखण्ड CB खींचा।
6. B₇ से रेखा B₇C’ || B₅C खींची जो BC को बढ़ाने पर C’ पर काटती है जिससे BC’ = 75 BC
7. C’ से C’A’ || CA खींची जो BA को बढ़ाने पर इसे A पर काटे जिससे A’B = 75 AB
∆A’BC’ अभीष्ट समरूप त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 7 : 5
BC’ : BC = 7 : 5
⇒ BC’ = 75 BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 7 : 5
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की 75 हैं।
इति सिद्धम्

प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 112 गुनी हों।
हल
दिया है : 8 cm आधार और 4 cm ऊँचाई का एक समद्विबाहु त्रिभुज।
रचना करनी है : उक्त समद्विबाहु त्रिभुज की और एक अन्य त्रिभुज की जिसकी भुजाएँ दिए हुए समद्विबाहु त्रिभुज की संगत भुजाओं की 32 हों।
रचना विधि :
1. रेखाखण्ड AB = 8 cm खींचा।
2. रेखाखण्ड AB का लम्ब समद्विभाजक खींचा जो AB को M पर काटता है।
3. M को केन्द्र मानकर समद्विभाजक में से MA = 4 cm काटा।
4. रेखाखण्ड AB व AC खींचकर समद्विबाहु त्रिभुज ABC प्राप्त किया।

5. BC को दोनों ओर बढ़ाया।
6. बिन्दु M पर BC से नीचे की ओर न्यूनकोण बनाती हुई रेखा MX खींची।
7. MX में से 3 समान भाग MM₁, M₁M₂, M₂M₃ खींचे।
8. रेखाखण्ड M₂C खींचा और M₃ से M₂C के समान्तर रेखा खींची जो बढ़ी हुई BC में C’ पर मिलती है।
9. C’ से AC के समान्तर C’A’ खींची जो MA से बिन्दु A’ पर मिलती है।
10. अब A से AB के समान्तर AB’ खींची जो बढ़ी हुई CB से B’ पर मिलती है।
ΔABC’ अभीष्ट त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 3 : 2
BC’ : BC = 3 : 2
⇒ BC’ = 32 BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 3 : 2
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की 32 हैं।
इति सिद्धम्

प्रश्न 5.
एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 34 गुनी हों।
हल
दिया है : एक त्रिभुज ABC जिसकी भुजा AB = 5 cm, BC = 6 cm और ∠ABC = 60° हैं।
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 32 गुनी हों।
रचना विधि :
1. रेखाखण्ड BC = 6 cm खींचा।
2. BC के बिन्दु B पर BC से 60° का B कोण बनाती हुई रेखा BY खींची।
3. BY में से AB = 5 cm काटी और रेखाखण्ड AC को खींचकर त्रिभुज ABC प्राप्त किया।

4. BC के दूसरी ओर बिन्दु B से BC पर न्यूनकोण बनाती हुई रेखा BX खींची।
5. BX में से चार समान भाग BB₁, B₁B₂, B₂B₃ और B₃B₄ खींचे।
6. B₄C खींची और B₃ से B₄C के समान्तर एक रेखा खींची जो BC से C” पर मिलती है।
7. C’ से AC के समान्तर रेखा C’A’ खींची जो AB से A’ पर मिलती है।
∆A’BC’ अभीष्ट त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 3 : 4
BC’ : BC = 3 : 4
⇒ BC’ = 34 BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 3 : 4
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की 34 हैं।
इति सिद्धम्

प्रश्न 6.
एक त्रिभुज ABC बनाइए जिसमें BC = 7 cm, ∠B = 45° व ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की भुजाओं की 43 गुनी हों।
हल
दिया है : ∆ABC जिसमें BC = 7 cm, ∠B = 45° व ∠A = 105°
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 43 गुनी हो।
रचना विधि :
1. रेखाखण्ड BC =7 cm खींचा।
2. BC के बिन्दु B पर BC से 45° का कोण बनाती हुई एक रेखा BZ खींची।
3. BC के दूसरी ओर B पर BC से 105° के कोण पर रेखा BD खींची।
4. BD के बिन्दु B पर BD से समकोण बनाती हुई एक रेखा BX खींची।
5. BC का लम्ब समद्विभाजक खींचा जो Bx को बिन्दु O पर काटती है।
6. O को केन्द्र मानकर OB त्रिज्या से वृत्तखण्ड BAC खींचा जो BZ को बिन्दु A पर काटता है।
7. AC को मिलाकर ∆ABC प्राप्त किया।

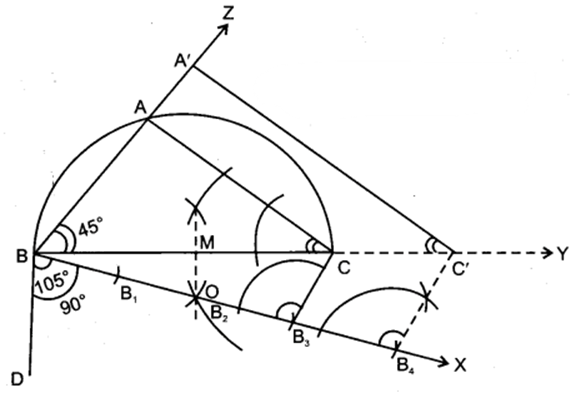
8. BX में से 4 समान खण्ड BB₁, B₁B₂, B₂B₃ व B₃B₄ खींचे।
9. रेखाखण्ड B₃C खींचा।
10. बिन्दु B₄ से B₄C’ समान्तर BC खींची जो बढ़ी हुई BC को C’ पर काटती है।
11. C’ से C’A’ समान्तर AC खींची जो BZ को A’ पर काटती है।
∆A’BC’ अभीष्ट त्रिभुज है।
औचित्य : क्योंकि BB₄, BB₃ की 43 गुनी है और BC || B₄C’
∴ BC’, BC की 43 गुनी होगी।
∵ A’C’ || AC और BC’ = 43 BC
∴ A’B भी AB की 43 गुनी है।
∴ A′BAB=A′C′AC=BC′BC=43
इति सिद्धम्

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm व 3 cm लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 53 गुनी हों।
हल
दिया है : समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाएँ 3 cm व 4 cm हों।
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ उक्त समकोण त्रिभुज की संगत भुजाओं की 53 गुनी हों।
रचना विधि :
1. रेखाखण्ड BC = 4 cm खींचा।
2. BC के बिन्दु B से BC पर लम्ब BY खींचा और उसमें से BA (या AB) = 3 cm काटी।
3. AC को मिलाया। इस प्रकार ∆ABC प्राप्त होगा।
4. BC के बिन्दु B पर BC से न्यूनकोण बनाती हुई रेखा BX खींची।
5. BX में से 5 समान भाग BB₁, B₁B₂, B₂B₃, B₃B₄ व B₄B₅ काटी।
6. B₃C को मिलाया।

7. B₅ से B₅C के समान्तर रेखा B₅C’ खींची जो बढ़ी हुई BC से C’ पर मिलती है।
8. C’ से C’A’ || CA खींची जो BY से A’ पर मिलती है।
∆A’BC’अभीष्ट त्रिभुज है।
औचित्य : ∵ BB₅, BB₃ की 53 गुनी है और B₃C || B₅C
BC’ = 53 BC और BC’ = 53 BC
तथा AC || AC’
A’B = 53 AB
अतः भुजाएँ A’B, BC’ व C’A’ क्रमश: AB, BC व CA की 53 गुनी है।
इति सिद्धम्