Chapter 9 – Sequences and Series (Ex – 9.4)

Sequences and Series (Ex – 9.4)

Find the sunt to n terms of each of the series in Exercises 1 to 7.

Question 1.
1 x 2 + 2 x 3 + 3 x 4 + 4 x 5 + ………

Solution:
In the given series, there is a sum of multiple of corresponding terms of two A.P’s. The two A.P’s are

Question 2.
1 x 2 x 3 + 2 x 3 x 4 + 3 x 4 x 5 + ……

Solution:

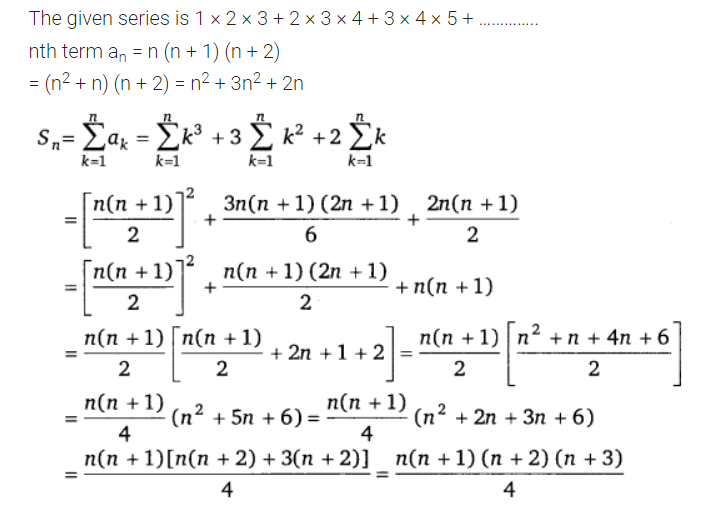
Question 3.
3 x 1² + 5 x 2² + 7 x 3² + …..

Solution:
In the given series there is sum of multiple of corresponding terms of two A.P’s. The two A.P’s are
(i) 3, 5, 7, …………… and
(ii) 1², 2², 3², ………………….
Now the n^th term of sum is an = (nth term of the sequence formed by first A.P.) x (n^th term of the sequence formed by second A.P.) = (2 n + 1) x n² = 2n³ + n² Hence, the sum to n terms is,

Question 4.

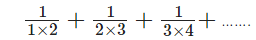
Solution:
In the given series there is sum of multiple of corresponding terms of two A.P’s. The two A.P’s are

Question 5.
5² + 6² + 7² + ………….. + 20²

Solution:
The given series can be written in the following way

Question 6.
3 x 8 + 6 x 11 + 9 x 25 + ………….

Solution:
In the given series, there is sum of multiple of corresponding terms of two A.P/s. The two A.P/s are
(i) 3, 6, 9, ………….. and
(ii) 8, 11, 14, ……………….
Now the nth term of sum is an = (n^th term of the sequence formed by first A.P.) x (n^th term of the sequence formed by second A.P.)

Question 7.
1² + (1² + 2²) + (1² + 2² + 3²) + ………….

Solution:
In the given series
a_n = 1² + 2² + …………….. + n²

Find the sum to n terms of the series in Exercises 8 to 10 whose n^th terms is given by

Question 8.
n(n + 1)(n + 4)

Solution:
We have

Question 9.
n² + 2ⁿ

Solution:
We have a_n = n² + 2ⁿ
Hence, the sum to n terms is,

Question 10.
(2n – 1)²

Solution:
We have