Chapter 6 – Triangles (Ex – 6.4)

Question 1.
Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.

Solution:

Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

Solution:
In ∆s AOB and COD, we have :
∠AOB = ∠COD [Vert.opp.∠s]
and ∠OAB = ∠OCD [Alternate ∠s]
∴ By AA criterion of similarity, we have:

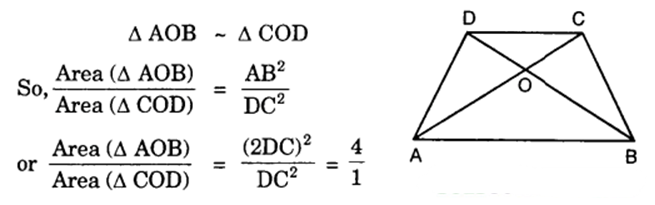
Hence, area (∆ AOB) : area (∆ COD) = 4 : 1

Question 3.
In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that

= AO/DO.

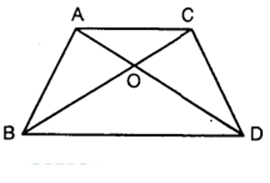
Solution:
Given : Two As ABC and DBC which stand on the same base BC but on the opposite sides of BC.
To prove :

= AO/DO.
Construction : Draw AE ⊥ BC and DF ⊥ BC.

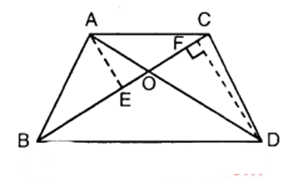
Proof:
In ∆s AOE and DOF, we have :
∠AEO = ∠DFO = 90°
∠AOE = ∠DOF [Vertically opp. ∠s]
∴ By AA criterion of similarity, we have :

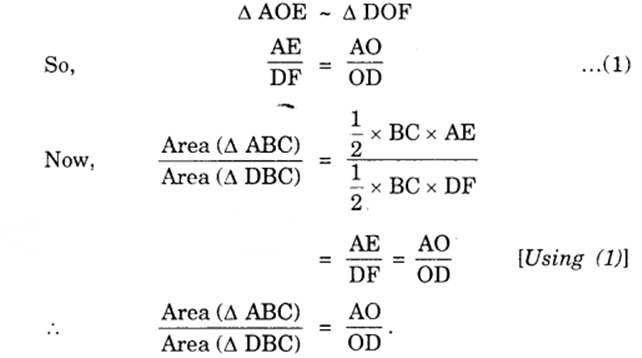
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.

Solution:
Given : Two ∆s ABC and DEF such that ∆ ABC – ∆ DEF
and Area (∆ ABC) = Area (∆ DEF)
To prove : ∆ ABC ≅ ∆ DEF

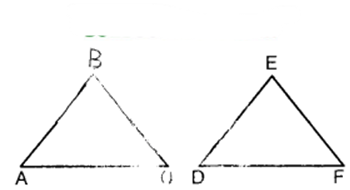
Proof:
∆ ABC ~ ∆ DEF
So, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
and AB/DE = BC/EF = AC/DF
To establish ∆ ABC ≅ ∆ DEF, it is sufficient to prove that

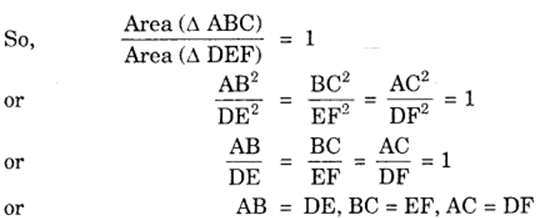
Hence ∆ ABC ≅ ∆ DEF [By SSS]

Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ ALBC. Find the ratio of the areas of ∆ DEF and ∆ ABC.

Solution:
Since D and E are respectively, the mid-points of the sides AB and BC of ∆ ABC, therefore
DE [| AC, or DE || FC … (1)
Since D and F are respectively the mid-points of the sides AB and AC
∆ ABC, therefore

DF || BC, or DF || EC … (2)
From (1) and (2), we can say that DECF is a parallelogram.
Similarly, ADEF is a parallelogram.
Now, in ∆s DEF and ABC, we have :
∠DEF = ∠A [Opp. Zs of ||gm ADEF]
and ∠EDF = ∠C [Opp. Zs of ||gm DECF]
∴ By AA criterion of similarity, we have :
∆ DE ≅ ∆ AC

Hence, Area (∆ DEF) : Area (∆ ABC) =1:4.

Question 6.
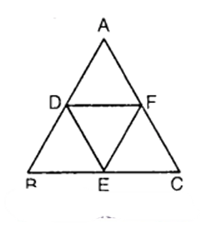
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Solution:
Given : ∆ ABC ~ ∆ PQR, AD and PM are the medians of ∆s ABC and PQR respectively.
To Prove :  Area (ΔABC)/Area (ΔPQR)=AD²/PM²
Proof : Since ∆ ABC ~ ∆ PQR, therefore

Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of the diagonals.

Solution:
Given : A square ABCD. Equilateral ∆s BCE and ACF have been drawn on side BC and the diagonal AC respectively.
To prove : Area (∆ BCE) = 12(Area ∆ ACF)

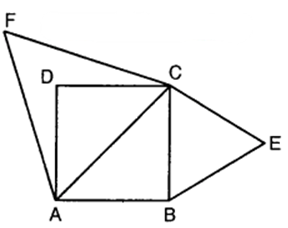
Proof: ∆ BCE ~ ∆ ACF [All equilateral triangles are similar]

Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is ____________.
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4

Solution:
Since ∆ ABC and ∆ BDE are equilateral triangles, they are equiangular and hence ∆ ABC – ∆ BDE

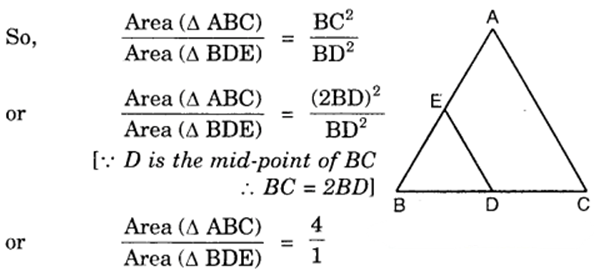
∴ (C) is the correct answer.

Question 9.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81

Solution:
Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides, therefore
ratio of areas = (4)² : (9)² = 16 : 81
∴ (D) is the correct answer.