Triangles
Question 1.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:
(i) Let a = 7 cm, b = 24 cm and c = 25 cm.
Here the largest side is c = 25 cm.
We have : a² + b² = 7² + 24²
= 49 + 576
= 625 = c²
So, the triangle with the given sides is a right triangle. Its hypotenuse is 25 cm.
(ii) Let a – 3 cm, 6 = 8 cm and c = 6 cm.
Here, the largest side is 6= 8 cm.
We have : a² + c² = 3² + 6²
= 9 + 36
= 45 ≠ b²
So, the triangle with the given sides is not a right triangle.
(iii) Let a = 50 cm, b – 80 cm and c = 100 cm.
Here, the largest side is c = 100 cm.
We have : a² + b² = 50² + 80²
= 2500 + 6400
= 8900 ≠ c²
So, the triangle with the given sides is not a right triangle.
(iv) Let a = 13 cm, b – 12 cm and c = 5 cm.
Here, the largest side is a = 13 cm.
We have : b² + c² = 12² + 5²
= 144 + 25
= 169 = a²
So, the triangle with the given sides is a right triangle. Its hypotenuse is 13 cm.
Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM.MR.
Solution:
Given : PQR is a triangle right angled at P and PM ⊥ QR.
To Prove : PM² = QM.MR
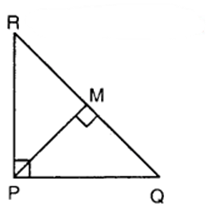
Proof: Since PM ⊥ QR, therefore
∆ PQM ~ ∆ RPM
or PM/QM = MR/PM
So, PM² = QM.MR.
Question 3.
In the figure, ABD is triangle right angled at and AC ⊥ BD. Show that
(i) Ab² = BC.BD
(ii) Ac² = BC.DC
(iii) AD² = BD.CD
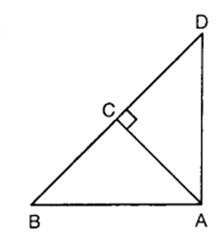
Solution:
Given : ABD is a triangle right angled at A and AC ⊥ BD.
To Prove :
(i) Ab² = BC.BD
(ii) Ac² = BC.DC
(iii) AD² = BD.CD
Proof:
(i) Since AC ⊥ BD, therefore
∆ ABC – ∆ DAC and each triangle is similar to the whole ∆ ABD.
∵ ∆ ABC – ∆ DBA
or AB/DB = BC/AB
∴ AB² = BC.BD
(ii) Since ∆ ABC ~ ∆ DAC, therefore
or AC/BC = DC/AC
∴ Ac² = BC.DC
(iii) Since ∆ ACD ~ ∆ BAD, therefore
or AD/CD = BD/AD
∴ AD² = BD. CD.
Question 4.
ABC is an isosceles triangle right angled at C. Prove that Ab² = 2Ac².
Solution:
Since ABC is an isosceles A right triangle, right angled at C, therefore
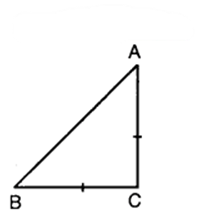
Ab² = Ac² + Bc²
or Ab² = Ac² + Ac² [∵ BC = AC, given]
So, Ab² = 2 Ac²
Question 5.
ABC is an isosceles triangle with AC = BC. If Ab² = 2Ac², prove that ABC is a right triangle.
Solution:
Since ABC is an isosceles triangle with AC = BC and Ab² = 2Ac², therefore
Ab² = Ac² + Ac²
or Ab² = Ac² + Bc² [∵ AC = BC, given]
∴ ∆ ABC is right angled at C.
Question 6.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:
Let ABC be an equilateral triangle of side 2a units. Draw AD ⊥ BC. Then, D is the mid-point of BC
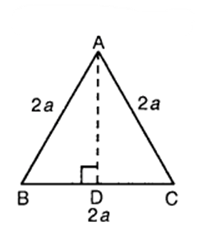
So, BD = 1/2 BC
= 1/2 x 2a = a
Since ABD is a right triangle, right angled at D, therefore
Ab² = AD² + BD²
or (2a)² = AD² + (a)²
or AD² = 4a² – a²
or AD2 = 3a²
or AD = √3a
∴ Each of its altitudes is √3a.
Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum o diagonals.
Solution:
Let the diagonals AC and BD of a rhombus ABCD intersect each other at O. Since the diagonals of a rhombus bisect each other at right angles.

∠AOB = ∠BOC – ∠COD
= ∠DOA = 90°
and AO = CO, BO = OD
Since AOB is a right triangle right
AB² = Oa² + Ob²
or AB² = (12AC)² +(12BD)² [∵ OA = OC and OB = OD]
or 4AB² = Ac² + BD² … (1)
Similarly, we have :
4BC² = Ac² + BD² …(2)
4CD² = Ac² + BD² …(3)
and 4AD² = Ac² + BD²
Adding all these results, we get
4(AB² + BC² + CD² + AD)² = 4(AC² + BD²)
or AB² + BC² + CD² + DA² = AC² + BD².
Question 8.
In the figure, O is a point in the interior of a triangle ABC, OD ± BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) Oa² + Ob² + Oc² – OD² – OE² – OF² B = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF².
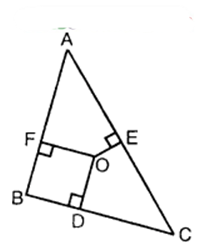
Solution:
Join AO, BO and CO.
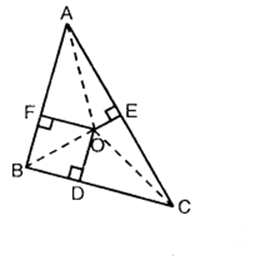
(i) In right As OFA, ODB and OEC, we have :
OA² = AF² + OF²
Ob² = BD² + OD²
and OC² = CE² + OE²
Adding all these, we get
OA² + OB² + OC² = AF² + BD² + CE² + OF² + OD² + OE²
or OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE².
(ii) In-right As ODB and ODC, we have :
OB² = OD² + BD²
and OC² = OD² + CD²
or OB² – OC² – BD² – CD² … (1)
Similarly, we have :
OC² – OA² = CE² – AE² … (2)
and OA² – OB² = AF² – BF² … (3)
Adding equations (1), (2) and (3), we get
(OB² – OC²) + (OC² – OA²) + (OA² – OB²)
= (BD² – CD²) + (CE² – AE²) + (AF² – BF²)
or (BD² + CE² + AF²) – (AE² + CD² + BF²) = 0
or AF² + BD² + CE²
= AE² + BF2 + CD².
Aliter for (ii) :
Taking triangles OFB, ODC and OAE, we have :
OA² + OB² + OC²- OD²- OE² – OF² = AE² + BF² + CD²
So, using result (i) above, we have :
AF² + BD² + CE² = AE² + BF² + CD²
Question 9.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Solution:
Let AB be the ladder, B be the B window and CB be the wall. Then, ABC is a right triangle, right angled at C.
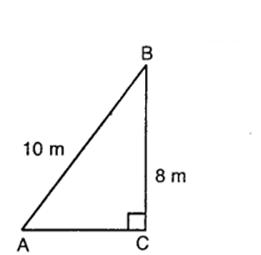
∴ AB² = AC² + Bc²
So, 10² = AC² + 8²
or AC² = 100 – 64
or AC²= 36
∴ AC = 6 .
Hence, the foot of the ladder is at a distance of 6 m from the base of the wall.
Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut ?
Solution:
Let AB (= 24 m) be a guy wire attached to a vertical pole BC of height 18 m. To keep the wire taut, let it be fixed to a stake at A. Then, ABC is a right triangle, right angled at C.
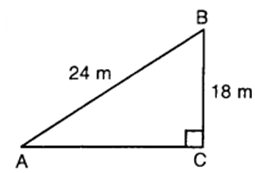
∴ AB² = AC²+ Bc²
So, 24² = AC²+ 182
or AC² = 576 – 324
or AC² = 252
or AC = √252 = 6√7
Hence, the stake may be placed at a distance of 6√7 m from the base of the pole.
Question 11.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 3/2 hours?
Solution:
Let the first aeroplane starts from O and goes upto A towards north, where OA = (1000 x 3/2) km = 1500 km.
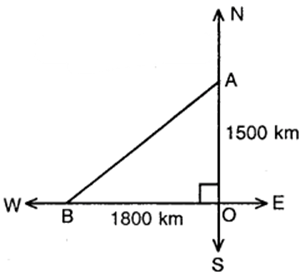
Let the second aeroplane starts from O at the same time and goes upto B towards west, where OB = (1200 x 3/2) km = 1800 km.
According to the problem, the required distance = BA.
∆In right angled ∆ ABC, by Pythagoras theorem, we have :
AB² = OA² + OB²
= (1500)² + (1800)² = 2250000 + 3240000
= 5490000 = 9 x 61 x 100 x 100
or AB = 3 x 100 √61 km = 300 √61 km.
Question 12.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:
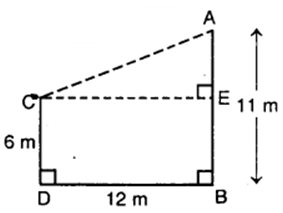
Let AB = 11 m and CD = 6 m be the two poles such that BD = 12 m.
Draw CE ⊥ AB and join AC.
∴CE = DB = 12 m,
AE = AB – BE
= AB – CD
= (11 – 6) m = 5 m.
In right angled ∆ ACE, by Pythagoras theorem, we have :
AC² = CE² + AE²
= (12)² + (5)² = 144 + 25 = 169
So, AC = √169 = 13
Hence, the distance between the tops of the two poles is 13 m.
Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
Solution:
In right angled ∆s ACE and DCB, we have :
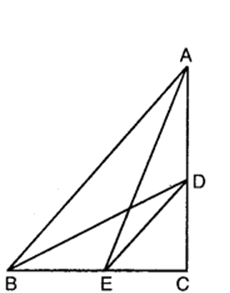
AE² = AC²+ CE²
and BD² = DC²+ Bc²
So, AE² + BD² = (AC²+ CE²) + (DC²+ Bc²)
AE² + BD² = (AC²+ Bc²) + (DC²+ CE²)
AE² + BD² = AB² + DE² [By Pythagoras theorem, AC²+ BC²= AB² and DC²+ CE² = DE²]
Question 14.
The perpendicular from A on side BC of a ∆ ABC intersects BC at D such that DB = 3 CD (see figure). Prove that 2AB² = 2AC²+ BC².
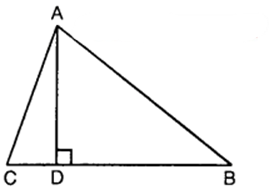
Solution:
We have : DB = 3CD
Now, BC = DB + CD
i.e., BC = 3CD + CD [∵ BD = 3CD]
or BC = 4CD
∴ CD = 1/4 BC and DB = 3CD = 3/4 BC … (1)
Since ∆ ABD is a right triangle, right angled at D, therefore by Pythagoras theorem, we have :
AB² = AB² + DB²
Similarly, from ∆ACD, we have :
AC² = AD² + CD²
(1) – (2) gives
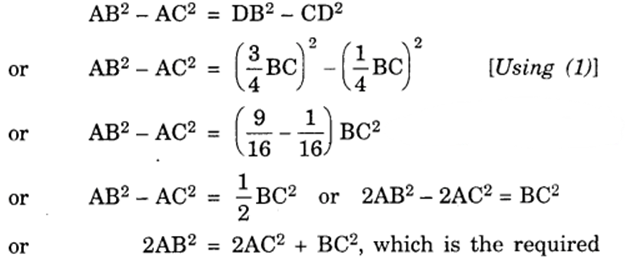
Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9AD² = 7AB².
Solution:
Let ABC be an equilateral triangle and let D be a point on BC such that
BD = 1/3BC.
Draw AE ⊥ BC. Join AD.
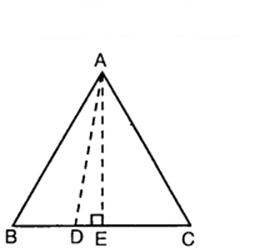
In ∆s AEB and AEC, we have :
AB = AC [∴∆ABC is equilateral]
∠AEB = ∠AEC [∵ Each = 90°]
and AE = AE
∴ By SAS criterion of congruence, we have :
∆ AEB = ∆ AEC
So, BE = EC
Now, we have :
BD = 1/3BC, DC = 2/3BC
BE = EC = 1/2BC … (1)
Since ∠C = 60°, therefore triangle.
∆ ADC is an acute triangle.
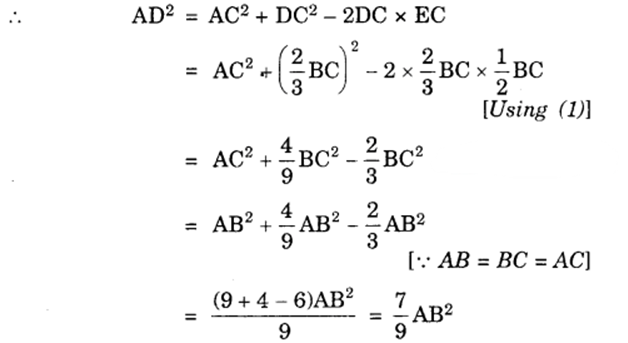
So, 9AD² = 7 AB², which is the required result.
Aliter:
DE = BE – BD
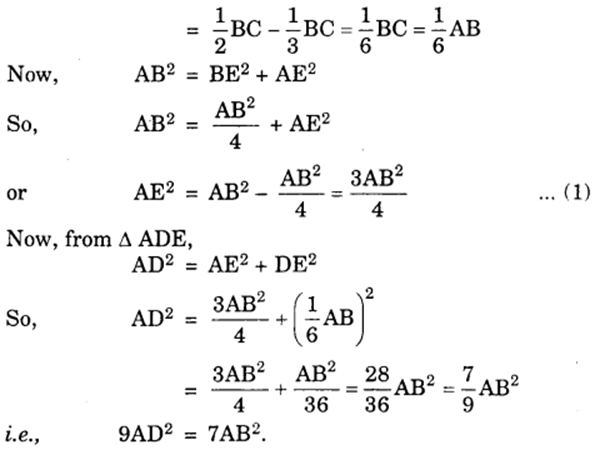
Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:
Let ABC be an equilateral triangle and let AD ⊥ BC. In ∆ ADB and ∆ ADC, we have :
AB = AC [Given]
AD = AD [Common]
and ∠ADB = ∠ADC [Each = 90°]
By RHS criterion of congruence, we have :
∆ ADB ≅ ∆ ADC
So, BD = DC or BD = DC = 12BC … (1)
Since ∆ ADB is a right triangle, right angled at D, by Pythagoras theorem, we have :
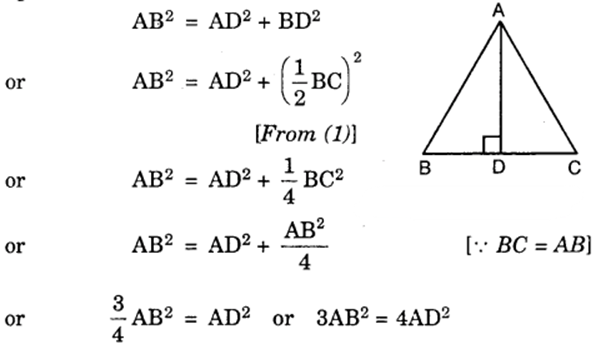
Hence, the result.
Question 17.
Tick the correct answer and justify :
In ∆ ABC, AB = 6√3cm, AC = 12 cm and BC = 6 cm. The angle B is :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution:
In ∆ ABC, we have :
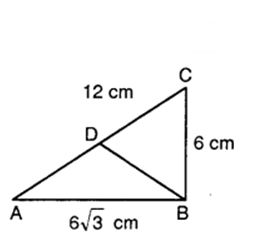
AB = 6√3 cm, AC = 12 cm
and BC = 6 cm … (1)
Now, AB² + BC²= (6√3)² + (6)² [From (1)]
= 36 x 3 + 36
= 108 + 36 = 144
= (AC)²
∴ Thus, ∆ ABC is a right triangle, right angled at B.
∠B = 90°
∴ (C) is the correct choice.
