Chapter 6 - त्रिभुज (Ex - 6.6)

त्रिभुज

प्रश्न 1.
दी गई आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि QSSR=PQPR है।

हल
दिया है : ∆PQR में PS कोण QPR का समद्विभाजक है।
सिद्ध करना है : QSSR=PQPR
रचना : बिन्दु R से रेखा RT || PS खींची जो बढ़ाई गई QP को T पर प्रतिच्छेद करे।
उपपत्ति : TR || PS और PR तिर्यक रेखा है
∠SPR = ∠PRT (एकान्तर कोण-युग्म है) ……(1)
पुन: TR || PS और QT तिर्यक रेखा है।
∠QPS = ∠PTR (संगत कोण-युग्म है) ……(2)
परन्तु PS, ∠QPR का समद्विभाजक है।
∠QPS = ∠SPR …….(3)
तब, समीकरण (1), (2) व (3) से,
∠PTR = ∠PRT
∆PTR की भुजा PT = PR ……(4)

अब, ∆QTR में, PS || TR
PQPT=QSSR
परन्त समीकरण (4) से, PT = PR
अतः PQPR=QSSR⇒QSSR=PQPR
इति सिद्धम्

प्रश्न 2.
दी गई आकृति में D, ∆ABC के कर्ण AC पर स्थित एक बिन्दु है जबकि BD ⊥ AC, DM ⊥ BC और DN ⊥ AB है। सिद्ध कीजिए कि-
(i) DM² = DN . MC
(ii) DN² = DM . AN

हल
दिया है : समकोण ∆ABC में ∠ABC = 90°
BD ⊥ AC, DM ⊥ BC तथा DN ⊥ AB
सिद्ध करना है :
(i) DM² = DN . MC
(ii) DN² = DM . AN
उपपत्ति : समकोण ∆ABC में, BD ⊥ AC (दिया है)
∆BDC ~ ∆ABC और ∆ADB ~ ∆ABC
जिससे ∆BDC ~ ∆ADB
तथा ∆BDC और ∆ADB समकोणीय हैं।
(i) समकोण ∆BDC में, DM ⊥ BC (दिया है)
∆DMC ~ ∆BMD
MCDM=DMBM
⇒ DM² = BM × MC …….(1)
चतुर्भुज BMDN में,
∠B = 90°, ∠M = 90° तथा ∠N = 90°
चतुर्भुज BMDN एक आयत है।
BM = DN ………(2)
तब, समीकरण (1) व (2) से,
DM² = DN . MC
इति सिद्धम्

(ii) समकोण ∆ADB में, DN ⊥ AB (दिया है)
∆AND और ∆DNB में,
DNBN=ANDN
⇒ DN² = BN . AN …….(3)
परन्तु, चतुर्भुज BMDN में,
∠B = 90°, ∠M = 90° तथा ∠N = 90°
चतुर्भुज BMDN एक आयत है।
BN = DM ……(4)
तब, समीकरण (3) व (4) से,
DN² = DM · AN
इति सिद्धम्

प्रश्न 3.
दी गई आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° तथा AD ⊥ CB है। सिद्ध कीजिए कि AC² = AB² + BC² + 2BC . BD है।

हल
दिया है : ∆ABC में, ∠ABC > 90° तथा AD ⊥ CB है।
सिद्ध करना है : AC² = AB² + BC² + 2BC . BD
उपपत्ति : समकोण ∆ABD में,
AB² = AD² + BD² ……(1)
पुनः समकोण ∆ACD में,
AC² = AD² + DC²
= AD² + (BD + BC)² (∵ DC = BD + BC)
= AD² + BD² + BC² + 2BC . BD [∴ (BD + BC)² के विस्तार से]
= AB² + BC² + 2BC . BD [∴ समीकरण (1) से ]
अतः AC² = AB² + BC² + 2BC . BD
इति सिद्धम्

प्रश्न 4.
दी गई आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° है तथा AD ⊥ BC है। सिद्ध कीजिए कि AC² = AB² + BC² – 2BC . BD है।

हल
दिया है : ∠B < 90° तथा AD ⊥ BC
सिद्ध करना है : AC² = AB² + BC² – 2BC . BD
उपपत्ति : AD ⊥ BC
∆ABD तथा ∆ACD समकोणीय त्रिभुज हैं।
तब, समकोण त्रिभुज ABD में,
AB² = AD² + BD² ……(1)
और समकोण त्रिभुज ACD में,
AC² = AD² + DC² …….(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
AC² – AB² = DC² – BD²
⇒ AC² – AB² = (DC + BD) (DC – BD) (∵ (a + b) (a – b) = a² – b²)
⇒ AC² – AB² = BC(DC – BD) (∵ DC + BD = BC)
⇒ AC² – AB² = BC(BC – BD – BD) (∵ DC = BC – BD)
⇒ AC² – AB² = BC (BC – 2BD)
⇒ AC² – AB² = BC² – 2BC × BD
अत: AC² = AB² + BC² – 2BC . BD
इति सिद्धम्

प्रश्न 5.
दी गई आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि-

हल
दिया है : ABC एक त्रिभुज है जिसमें D, भुजा BC का मध्य-बिन्दु AM, BC पर लम्ब खींचा गया है और AC > AB
सिद्ध करना है :

उपपत्ति : (i) समकोण ∆AMD में, AM² + DM² = AD² …..(1)
समकोण ∆AMC में,
AC² = AM² + MC²
= (AD² – DM²) + MC² [समीकरण (1) से AM² = AD² – DM²]
= AD² – DM² + (DM + DC)² [∵ MC = DM + DC]
= AD² – DM² + DM² + 2DM . DC + DC²
= AD² + 2 DM . DC + (12 BC)² [∵ D, BC मध्य-बिन्दु है]
= AD² + (2DC). DM + 14 BC² [∵ 2DC = BC]
अत: AC² = AD² + BC . DM + (BC2)2 ……(2)
इति सिद्धम्

(ii) समकोण ∆AMB में,
AB² = AM² + BM²
= (AD² – DM²) + BM²
= AD² – DM² + (BD – DM)²
= AD² – DM² + BD² – 2BD . DM + DM² [∵ (a – b)² = a² – 2ab + b²]
= AD² – 2BD . DM + BD²
= AD² – BC . DM + (12BC)2 [∵ D, BC का मध्य-बिन्दु है।]
AB² = AD² – BC . DM + 14 BC² …….(3)
अत: AB² = AD² – BC . DM + (BC2)2
इति सिद्धम्

(iii) खण्ड (i) व खण्ड (ii) के परिणामों का योग करने पर,
AB² + AC² = 2AD² + 2 . 14 BC² = 2AD² + 12 BC²
अत: AB² + AC² = 2AD² + 12 BC²
इति सिद्धम्

प्रश्न 6.
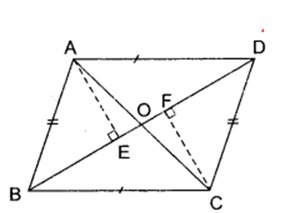
सिद्ध कीजिए कि एक समान्तर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।

हल
दिया है : ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण AC और BD परस्पर बिन्दु O पर काटते हैं।
सिद्ध करना है : AC² + BD² = AB² + BC² + CD² + DA²
रचना : A से BD पर AE C से BD पर CF लम्ब खींचा।
उपपत्ति: ABCD एक समान्तर चतुर्भुज है और AC तथा BD उसके विकर्ण हैं जो परस्पर O पर काटते हैं।
∴ AO = OC, OB = OD तथा AB = CD
तब, समकोण ∆ABE में,

प्रश्न 7.
दी गई आकृति में एक वृत्त की दो जीवाएँ AB और CD परस्पर बिन्द P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC ~ ∆DPB
(ii) AP . PB = CP . DP

हल
दिया है : एक वृत्त की AB व CD दो जीवाएँ हैं जो एक-दूसरे को बिन्दु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है :
(i) ∆APC ~ ∆DPB
(ii) AP . PB = CP . DP
रचना : रेखाखण्ड AD व CB खींचे।
उपपत्ति : (i) जीवा AB और CD परस्पर P पर काटती हैं।
शीर्षाभिमुख कोण ∠APC = ∠BPD
∠CAP = ∠BDP (एक ही वृत्तखण्ड के कोण हैं)
और ∠ACP = ∠DBP (एक ही वृत्तखण्ड के कोण हैं)

अब, ∆APC और ∆BPD में,
∠APC = ∠BPD
∠CAP = ∠BDP
∠ACP = ∠DBP
दो त्रिभुजों की समरूपता की कसौटी AAA से,
∆APC ~ ∆DPB
इति सिद्धम्
(ii) ∆APC और ∆DPB में,
APDP=CPPB
अत: AP . PB = CP . DP
इति सिद्धम्

प्रश्न 8.
दी गई आकृति में एक वृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC ~ ∆PDB
(ii) PA . PB = PC . PD

हल
दिया है : AB और CD एक वृत्त की दो जीवाएँ हैं जो बढ़ाने पर एक-दूसरे को वृत्त के बाहर बिन्दु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है :
(i) ∆PAC ~ ∆PDB
(ii) PA . PB = PC . PD
रचना : रेखाखण्ड AC व BD को मिलाया।
उपपत्ति : (i) चतुर्भुज ABCD एक चक्रीय चतुर्भुज है और ∠PAC उसका बहिष्कोण है।
∠PAC = ∠BDC
⇒ ∠PAC = ∠BDP
इसी प्रकार, ∠PCA, चक्रीय चतुर्भुज ABCD का बहिष्कोण है।
∠PCA = ∠ABD
∠PCA = ∠PBD …..(2)
अब, ∆PAC और ∆PBD में,
∠CPA = ∠BPD (दोनों त्रिभुजों का उभयनिष्ठ कोण है)
∠PAC = ∠BDP [समीकरण (1) से]
∠PCA = ∠PBD [समीकरण (2) से]
दो त्रिभजों की समरूपता के गुणधर्म AAA से,
∆PAC ~ ∆PDB
इति सिद्धम्
(ii) ∵ ∆PAC ~ ∆PDB
PAPD=PCPB
⇒ PA . PB = PC . PD
इति सिद्धम्

प्रश्न 9.
दी गई आकृति में त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि BDCD=ABAC है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।

हल
दिया है : ∆ABC की भुजा BC पर एक बिन्दु D ऐसा है कि BDCD=ABAC
सिद्ध करना है : AD, ∠BAC का समद्विभाजक है।
रचना : BA को उसकी सीध में E तक इतना बढ़ाया कि AE = AC हो। रेखाखण्ड CE खींचा।
उपपत्ति: दिया है,
BDCD=ABAC
∵ AC = AE ⇒ BDCD=ABAE
तब, ∆BEC में, BDCD=ABAE
अनुपातिकता के मूलभूत प्रमेय के विलोम से, AD || EC
AD || EC और BE तिर्यक रेखा है।
∠BAD = ∠AEC ……(1)
AD || EC और AC तिर्यक रेखा है।
∠CAD = ∠ACE ……(2)

परन्तु ∆ACE में रचना से, AC = AE
∠AEC = ∠ACE …….(3)
तब समीकरण (1), (2) व (3) से,
∠BAD = ∠CAD
परन्तु ∠BAD + ∠CAD = ∠BAC
अत: AD, ∠BAC का समद्विभाजक है।
इति सिद्धम्

प्रश्न 10.
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी की सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी की सतह पर स्थित बिन्दु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है? यदि वह डोरी को 5 cm/s की दर से अन्दर खींचे तो 12 सेकण्ड के बाद नाज़िमा की काँटे से क्षैतिज दूरी कितनी होगी?

हल
चित्र में, नाजिमा की मछली पकड़ने वाली छड़ का सिरा A पानी की सतह से 1.8 m ऊँचाई पर है जिससे AC = 1.8 m है।
डोरी AB के सिरे B पर एक काँटा है जिसकी बिन्दु C से दूरी BC = 2.4 m है और नाजिमा से B की दूरी BD = 3.6 m है।
CD = BD – BC = 3.6 – 2.4 = 1.2 m
माना डोरी की लम्बाई AB है।

तब समकोण ∆ABC में,
AB² = BC² + CA²
⇒ AB² = (2.4)² + (1.8)² = 5.76 + 3.24 = 9.0
⇒ AB = √9.00 = 3 m
अतः डोरी की लम्बाई = 3 m
जब वह डोरी को 5 cm/s की दर से अन्दर खींच रही है तो 12 सेकण्ड में खींची दूरी = 5 × 12 = 60 cm = 0.6 m
तब पानी के बाहर डोरी की लम्बाई AP = 3.6 – 0.6 = 2.4 m
तब काँटे से छड़ के सिरे A के ठीक नीचे बिन्दु C की क्षैतिज दूरी PC होगी।
समकोण ∆APC में,
PC² + AC² = AP²
PC² + (1.8)² = (2.4)²
PC² + 3.24 = 5.76
PC² = 5.76 – 3.24 = 2.52
PC = √2.52 = 1.587 m = 1.59 मीटर (लगभग)
काँटे से नाज़िमा की क्षैतिज दूरी PD = PC + CD = (1.59) + (1.2) cm = 2.79 m
अत: काँटे से नाज़िमा की क्षैतिज दूरी = 2.79 m