Chapter 3 – Trigonometric Functions (Ex – 3.3)

Trigonometric Functions (Ex – 3.3)

Question 1.
Prove that: sin²π/6+cos²π/3−tan²π/4=−1/2

Solution.
L.H.S. = sin²π/6+cos²π/3−tan²π/4
=[(1/2)²+(1/2)²−(1)²]
=1/4+1/4−1
=−1/2=R.H.S.

Question 2.

Solution.

Question 3.

Solution.

Question 4.

Solution.

Question 5.
Find the value of:
(i) sin 75°
(ii) tan 15°
Solution.
(i) sin (75°) = sin (30° + 45°)

(ii) tan 15° = tan (45° – 30°)

Prove the following:

Question 6.

Solution.
We have,

Question 7.

Solution.
We have,

Question 8.

Solution.
We have,

Question 9.

Solution.
We have,

Question 10.
sin(n +1 )x sin(n + 2)x + cos(n +1 )x cos(n + 2)x = cosx

Solution.
We have,

Question 11.

Solution.
We have,

Question 12.
sin²6x – sin²4x= sin²x sin10x

Solution.

Question 13.
cos²2x – cos²6x = sin 4x sin 8x

Solution.

Question 14.
sin2x + 2 sin 4x + sin 6x = 4 cos² x sin 4x

Solution.
We have,

Question 15.
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

Solution.

Question 16.

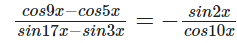
Solution.
We have,

Question 17.

Solution.
We have,

Question 18.

Solution.

Question 19.

Solution.

Question 20.

Solution.

Question 21.

Solution.

Question 22.
cot x cot 2x – cot 2x cot 3x – cot3x cotx = 1

Solution.
We know that 3x = 2x + x.
Therefore,

Question 23.

Solution.

Question 24.
cos 4x = 1 – 8 sin²x cos²x

Solution.

Question 25.
cos 6x = 32 cos6 x – 48 cos⁴x + 18 cos² x -1

Solution.