Chapter 9 - त्रिकोणमिति के कुछ अनुप्रयोग (Additional Questions)

त्रिकोणमिति के कुछ अनुप्रयोग

बहुविकल्पीय प्रश्न

प्रश्न 1.
जिस वक्त सूर्य का उन्नयन कोण 45° था, तब एक स्तम्भ की परछाई 10 m मापी गई। उस स्तम्भ की ऊँचाई थी
(i) 5 m
(ii) 10 m
(iii) 15 m
(iv) 20 m
हल
(ii) 10 m

प्रश्न 2.
10 m ऊँचे मकान के आधार से 10 m दूर स्थित बिन्दु से देखने पर उसकी छत का उन्नयन कोण होगा
(i) 60°
(ii) 45°
(iii) 30°
(iv) 75°
हल
(ii) 45°

प्रश्न 3.
यदि एक वृक्ष के आधार से 15 m दूर स्थित बिन्दु पर उसकी चोटी का उन्नयन कोण 30° बनता है, तो वृक्ष की ऊँचाई होगी।
(i) 15 m
(ii) 30 m
(iii) 15√3 m
(iv) 5√3 m
हल
(iv) 5√3 m

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
किसी समय कोई स्तम्भ की छाया की लम्बाई उसकी ऊँचाई की √3 गुनी है। सूर्य का उन्नयन कोण ज्ञात कीजिए।
हल
माना स्तम्भ AB की ऊँचाई h है, तब
छाया BC की लम्बाई = h√3
तथा उन्नयन कोण ∠ACB = θ

समकोण ∆ABC में,
tan θ = ABBC=hh3√=13√
⇒ tan θ = tan 30°
⇒ θ = 30°
अत: सूर्य का उन्नयन कोण 30° है।

प्रश्न 2.
एक वृक्ष का ऊपरी भाग टूटकर भूमि से जा लगा तथा भूमि से 45° का कोण बनाता है। यदि वृक्ष की जड़ से उस बिन्दु जहाँ वृक्ष का शिखर भूमि को छूता है, की दूरी 6 m है, तो वृक्ष की ऊँचाई ज्ञात कीजिए।
हल
माना A वृक्ष ABC का पाद है तथा BC वृक्ष का टूटा हुआ भाग है तथा C पेड़ का ऊपरी सिरा है।
तब ∠ACB = 45°
तथा ∠BAC = 90°
प्रश्नानुसार, AC = 6 m

समकोण ∆BAC में, tan 45° = ABAC
⇒ AB = AC tan 45° = 6 × 1 = 6 m
पुनः समकोण ∆BAC में, cos 45° = ACBC
⇒ BC = AC sec 45° = 6√2
∴ पेड़ की कुल माप = AB + BC = 6 + 6√2 = 6(√2 + 1) m

प्रश्न 3.
एक मीनार की चोटी का उन्नयन कोण उस मीनार के आधार से क्षैतिज तल पर 40 m दूरी पर स्थित बिन्दु से देखने पर 45° है। मीनार की ऊँचाई ज्ञात कीजिए।
हल

माना AB मीनार तथा बिन्दु C क्षैतिज तल पर मीनार के आधार से 40 m दूर स्थित बिन्दु है।
तब ∠ACB = 45°
समकोण ∆ABC में, tan 45° = ABBC
⇒ 1 = AB40
⇒ AB = 40 m
अत: मीनार की ऊँचाई 40 m है।

प्रश्न 4.
एक मीनार क्षैतिज समतल पर ऊर्ध्वाधरतः खड़ी है। यदि सूर्य का उन्नयन कोण 30° और मीनार की छाया की लम्बाई 45 m हो, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल
माना PQ ऊर्ध्वाधर मीनार तथा QR इसकी छाया है।
माना मीनार की ऊँचाई h है।
सूर्य का उन्नयन कोण, ∠PRQ = 30°

तब समकोण ∆PQR में,
tan 30° = PQRQ
⇒ PQ = RQ tan 30°
⇒ h = 45 × 13√ = 15√3 m

लघु उत्तरीय प्रश्न

प्रश्न 1.
एक मीनार के आधार से एक सरल रेखा में 100 m तथा 150 m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर का उन्नयन कोण पूरक कोण है। सिद्ध कीजिए कि मीनार की ऊँचाई 50√6 m है।
हल
AB एक मीनार है जिसकी ऊँचाई h m है। इसके आधार B से 100 m तथा 150 m दूरी पर दो बिन्दु C और D हैं जहाँ पर शिखर के उन्नयन कोण क्रमशः θ तथा (90° – θ) हैं।

अत: मीनार की ऊँचाई = 50√6 m
इति सिद्धम्

प्रश्न 2.
भूमितल पर दो बिन्दु A तथा B किसी मीनार के एक ही ओर स्थित हैं। यदि A तथा B पर मीनार के शिखर के उन्नयन कोण क्रमश: 30° तथा 60° हैं। यदि मीनार की ऊँचाई 150 m है, तो A तथा B के मध्य दूरी ज्ञात कीजिए।
हल
माना PQ एक मीनार है जिसकी ऊँचाई 150 m है। मीनार के पाद Q से जाने वाली क्षैतिज रेखा पर दो बिन्दु A और B हैं, जहाँ से मीनार की चोटी P से उन्नयन कोण क्रमशः 30° तथा 60° हैं।

प्रश्न 3.
भूमि पर किसी बिन्दु से एक हवाई जहाज का उन्नयन कोण 60° है। 15 s की उड़ान के पश्चात् उन्नयन कोण बदलकर 30° हो जाता है। यदि हवाई जहाज 1500√3 m की नियत ऊँचाई पर उड़ रहा है, तो हवाई जहाज की चाल किमी प्रति घण्टा में ज्ञात कीजिए।
हल
माना हवाई जहाज 15 सेकण्ड में C से D तक पहुँच जाता है।
समकोण ∆ABC में,

⇒ CD + BC = 1500√3 × √3 = 4500
⇒ CD + 1500 = 4500 [∵ BC = 1500 m]
⇒ CD = 4500 – 1500 = 3000 m
प्रश्नानुसार, हवाई जहाज को 3000 m जाने में 15 s लगते हैं।
अतः चाल = 300015 = 200 m/s
= 200×60×601000
= 720 km/h
अतः हवाई जहाज की चाल = 720 km/h

प्रश्न 4.
एक मीनार के शिखर से 50 m ऊँचे भवन के शिखर तथा पाद के अवनमन कोण क्रमशः 30° तथा 60° हैं। मीनार की ऊँचाई तथा भवन और मीनार के बीच की क्षैतिज दूरी ज्ञात कीजिए।
हल
माना AB भवन तथा CD मीनार है।
भवन तथा मीनार के बीच क्षैतिज दूरी BC = x (माना)
तथा मीनार की ऊँचाई CD = y (माना)
DX क्षैतिज रेखा है तथा AE, CD पर लम्ब है।
प्रश्नानुसार, ∠ADX = 30°
⇒ ∠DAE = 30° तथा ∠BDX = 60°
⇒ ∠DBC = 60°

समकोण ∆ADE में, cot 30° = AEED
√3 = xCD−CE (∵ AE = BC = x)
x = √3 (CD – AB) (∵ EC = AB)
x = √3(y – 50) ……(1)
पुनः समकोण ∆BCD में, cot 60° = BCCD

अत: मीनार की ऊँचाई 75 m तथा मीनार व भवन के बीच क्षैतिज दूरी 25√3 m

प्रश्न 5.
एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः 30° और 45° हैं। यदि पुल किनारों से 3 m की ऊँचाई पर हो तो नदी की चौड़ाई ज्ञात कीजिए।
हल
माना PQ नदी की चौड़ाई है। माना A नदी के पुल का एक बिन्दु है अर्थात् AB = 3 m
A से नदी के सम्मुख किनारों P और Q अवनमन कोण क्रमश: 30° और 45° हैं।

समकोण ∆ABQ में,
tan 45° = ABBQ
⇒ 1 = 3BQ
⇒ BQ = 3 m
पुनः समकोण ∆ABP में,
tan 30° = ABBP
⇒ 13√=3BP
⇒ BP = 3√3 m
अतः नदी की चौड़ाई = PQ = BP + BQ
= (3√3 + 3) m
= 3(√3 + 1) m
= 3(1.732 + 1) m
= 3(2.732) m
= 8.196 m
≅ 8.20 m

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
किसी बिन्दु पर एक मीनार के शिखर के उन्नयन कोण की स्पर्शज्या (tangent) 74 है। मीनार की ओर 25 m चलने पर उन्नयन कोण की स्पर्शज्या हो जाती है। मीनार की ऊँचाई ज्ञात कीजिए।
हल
माना मीनार PQ के धरातल पर बिन्दु A से 25 m दूर (मीनार की ओर) बिन्दु B है।
यदि ∠PAB = α तथा ∠PBQ = β

तब प्रश्नानुसार, tan α = 74 व tan β = 73
माना मीनार की ऊँचाई h है तो

अत: मीनार की ऊँचाई 175 m है।

प्रश्न 2.
एक व्यक्ति नदी के किनारे खड़े होकर देखता है कि नदी के दूसरे किनारे पर एक पेड़ के शीर्ष का उन्नयन कोण 60° है। जब वह किनारे से 21 m पीछे की ओर चलता है, तो वह उन्नयन कोण 30° पाता है। पेड़ की ऊँचाई तथा नदी की चौड़ाई ज्ञात कीजिए।
हल

माना AB पेड़ व BC नदी है। माना AB = h m व BC = x m
ज्ञात है ∠ACB = 60°
यदि किनारे C से 20 मीटर पीछे की ओर बिन्दु D है।
तब ∠ADB = 30°
समकोण ∆ABC में,
tan 60° = hx
⇒ √3 = hx
⇒ h = x√3 …….(1)
पुन: समकोण ∆ABD में,
tan 30° = ABBD=hx+20 ……(2)
⇒ 13√=x3√x+20 [समीकरण (1) से]
⇒ x + 20 = 3x
⇒ 2x = 20
⇒ x = 10
समीकरण (1) से, h = 10√3
अत: पेड़ की ऊँचाई 10√3 m तथा नदी की चौड़ाई 10 m है।

प्रश्न 3.
एक मनुष्य पानी के जहाज की छत जो पानी की सतह से 10 m ऊपर है, पर खड़ा है। वहाँ से पहाड़ी की चोटी का उन्नयन कोण 60° तथा पहाड़ की तली का अवनमन कोण 30° है। जहाज से पहाड़ी की दूरी और पहाड़ी की ऊँचाई ज्ञात कीजिए।
हल

माना AB एक जहाज तथा CD एक पहाड़ी है। पहाड़ी की चोटी का उन्नयन कोण ∠CAE = 60°
तथा पहाड़ी की तली का अवनमन कोण ∠EAD = 30° है।
जबकि AE, A से CD पर लम्ब है।
माना पहाड़ी की ऊँचाई h m और जहाज से पहाड़ी की दूरी x m है।
CE = (h – 10) m
समकोण ∆AED में, tan 30° = EDAE
13√=10x
x = 10√3 m [∵ AB = ED = 10 m]
पुनः समकोण ∆CEA में, tan 60° = CEAE
⇒ √3 = h−10x
⇒ √3 = h−10103√
⇒ h – 10 = 10 × 3 = 30
⇒ h = 30 + 10 = 40 m
अतः जहाज से पहाड़ी की दूरी 10√3 m तथा पहाड़ी की ऊँचाई 40 m है।

प्रश्न 4.
एक मकान के आधार से 30 m दूरस्थ एक मीनार के शिखर का उन्नयन कोण 60° तथा मकान की छत से उसी मीनार के शिखर का उन्नयन कोण 45° है। मकान तथा मीनार की ऊँचाई ज्ञात कीजिए।
हल

माना AB मकान तथा PQ मीनार है।
तब प्रश्नानुसार, BQ = 30 m,
∠PBQ = 60° तथा ∠PAM = 45°
माना मीनार की ऊँचाई H तथा मकान की ऊँचाई h है।
समकोण ∆PRB में, tan 60° = PQBQ=H30
⇒ √3 = H30
⇒ H = 30√3 m
पुन: समकोण ∆PMA में,
tan 45° = PMAM=PQ−MQAM
⇒ 1 = H−h30
⇒ H – h = 30
⇒ h = H – 30 = 30√3 – 30 = 30(√3 – 1) m
अत: मकान की ऊँचाई 30(√3 – 1) m तथा मीनार की ऊँचाई 303 m है।

प्रश्न 5.
किसी मीनार के आधार से a और b दूरी पर एक ही रेखा में स्थित दो बिन्दुओं क्रमशः A और B से देखने पर मीनार के ऊपरी सिरे के उन्नयन कोण पूरक पाये जाते हैं। सिद्ध कीजिए कि मीनार की ऊँचाई √ab है।
हल

माना मीनार OC की ऊँचाई = h m तथा मीनार का आधार OA है।
माना आधार पर (एक ही रेखा पर) दो बिन्दु A तथा B इस प्रकार हैं कि
OA = a तथा OB = b
क्योंकि A तथा B पर बनने वाले कोण पूरक हैं।
अत: यदि ∠CAO = θ
तब ∠CBO = 90° – θ
समकोण ∆COA में,

प्रश्न 6.
सड़क के एक ओर स्थित मकान के, सड़क के दूसरी ओर स्थित मीनार के शिखर से मकान की छत और आधार के अवनमन कोण क्रमश: 45° और 60° हैं। यदि मकान की ऊँचाई 10 m है, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल
माना AB मीनार तथा CD मकान है।
माना BD = x तथा मीनार की ऊँचाई = h m

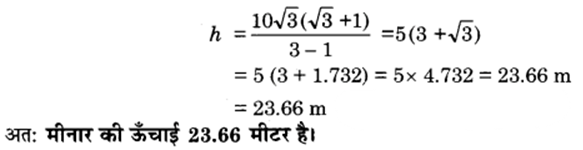
प्रश्न 7.
एक ऊर्ध्वाधर खम्भा (जो 100 dm से अधिक लम्बा है) दो भागों में बँटा है, जिसमें नीचे का भाग उसकी कुल लम्बाई का 13 है। यदि खम्भे की जड़ से 40 dm दूर एक स्थान पर उसका ऊपरी भाग कोण α अन्तरित करे (जबकि tan α = 12) तो खम्भे की लम्बाई ज्ञात कीजिए।
हल

माना उर्ध्वाधर खम्भा AB जिसकी ऊँचाई h है जो दो भागों AC व BC में बँटा है।
जबकि BC = 13 h
खम्भे की जड़ से 40 dm की दूरी पर बिन्दु D है।
तब ∠ADC = α माना ∠CDB = β
समकोण ∆CBD में,

⇒ 240h – h² = 4800 + 80h
⇒ h² – 160h + 4800 = 0
⇒ h² – 120h – 40h + 4800 = 0
⇒ h(h – 120) – 40(h – 120) = 0
⇒ (h – 120) (h – 40) = 0
⇒ h = 120
⇒ h = 40 जो कि मान्य नहीं है।
खम्भे की लम्बाई = 120 dm

प्रश्न 8.
एक अपूर्ण मन्दिर के आधार से 30 m दूर स्थित किसी बिन्दु से उसके शिखर का उन्नयन कोण 30° है। मन्दिर कितना ऊँचा और बनाया जाये कि उसी बिन्दु पर उन्नयन कोण 45° हो जाये (दिया है, √3 = 1.732)।
हल
माना बिन्दु D से देखने पर अपूर्ण मन्दिर AB के शिखर B का उन्नयन कोण 30° है।
∠BDA = 30°
माना मन्दिर की ऊँचाई BC बढ़ाने पर उसके शिखर C का उन्नयन कोण 45° हो जाता है।

∴ BC = AC – AB = 30 – 17.32 = 12.68 m
अत: मन्दिर को 1268 m ऊँचाई तक और बनवाना पड़ेगा।

प्रश्न 9.
मीनार PN पर एक स्तम्भ QP गड़ा है। मीनार के आधार N से 40 m की क्षैतिज दूरी पर एक बिन्दु A है। बिन्दु A पर मीनार PN और स्तम्भ QP के द्वारा अन्तरित कोण क्रमशः θ और Φ इस प्रकार हैं कि tan θ = 12 और tan Φ = 13 स्तम्भ की ऊँचाई ज्ञात कीजिए।
हल

∴ स्तम्भ PQ की ऊँचाई = QN – PN = 40 – 20 = 20 m

प्रश्न 10.
एक नाव से जो पुल की ओर आ रही है, उस पुल का उन्नयन कोण 30° देखा गया। नाव के उसी चाल से 6 min पश्चात् उन्नयन कोण 60° हो गया। ज्ञात कीजिए नाव को उस पुल तक उसी चाल से पहुँचने में कितना समय और लगेगा?
हल
माना P पुल है और नाव की प्रथम स्थिति A है जहाँ से पुल P का उन्नयन कोण 30° है।
6 m बाद नाव की द्वितीय स्थिति B है जहाँ से पुल का उन्नयन कोण 60° है।

माना AB = x, BQ = y तथा PQ = h
समकोण ∆PBQ में, tan 60° = hy
⇒ √3 = hy
⇒ h = y√3 …….(1)
समकोण ∆PAQ में, tan 30° = hx+y
⇒ 13√=hx+y
⇒ h√3 = x + y …….(2)
समी० (1) से h का मान समी० (2) में रखने पर,
y√3 . √3 = x + y
⇒ 3y = x + y
⇒ 3y – y = x
⇒ 2y = x
⇒ y = x2 m
∵ इकाई दूरी जाने में लगा समय = 6 min
∴ 1 इकाई दूरी जाने में लगा समय = 6x min
∴ x2 इकाई दूरी जाने में लगा समय = 6x×x2 = 3 min
अत: नाव को पुल तक पहुँचने में 3 min का समय और लगेगा।

प्रश्न 11.
एक वायुयान दो मकानों के ऊपर से उड़ रहा है जिनके बीच की न्यूनतम दूरी 300 m है। यदि किसी समय वायुयान से एक ही दिशा में दोनों मकानों के अवनमन कोण क्रमशः 45° और 60° हैं, तो ज्ञात कीजिए कि वायुयान कितनी ऊँचाई पर उड़ रहा है?
हल

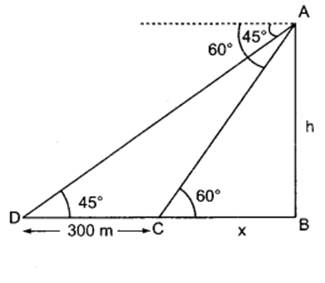
माना वायुयान A की ऊँचाई AB है।
तथा C व D क्रमश: दो मकान हैं जबकि CD = 300 m
माना वायुयान की ऊँचाई h है तथा BC = x
तब समकोण ∆ABC में,

प्रश्न 12.
एक हवाई जहाज जो कि 1000 m की ऊँचाई पर उड़ रहा है, पर स्थित मनुष्य उत्तर की ओर एक शत्रु की पनडुब्बी को 30° के अवनमन कोण पर तथा दक्षिण की ओर एक युद्धपोत को 45° के अवनमन कोण पर देखता है। पनडुब्बी और युद्धपोत के बीच की दूरी ज्ञात कीजिए।
हल

माना हवाई जहाज की स्थिति A, पनडुब्बी की स्थिति Bव युद्धपोत की स्थिति C है तब प्रश्नानुसार,
∠ABC = 30°, ∠ACB = 45°
तथा AO = 1000 m (जबकि AO ⊥ BC)
समकोण ∆AOC में, tan 45° = AOOC
⇒ 1 = 1000OC
⇒ OC = 1000
पुनः समकोण ∆AOB में,
tan 30° = AOBO
13√=1000BO
BO = 1000√3
∴ पनडुब्बी व युद्धपोत के बीच की दूरी, BC = (BO + OC)
= (1000√3 + 1000)
= 1000(√3 + 1) m

प्रश्न 13.
क्षैतिज सड़क के ऊर्ध्वाधर स्थित हवाई जहाज से सड़क के दो क्रमागत किलोमीटर के पत्थरों के जो हवाई जहाज के दोनों ओर स्थित हैं; अवनमन कोण α और β हैं। सिद्ध कीजिए कि हवाई जहाज की ऊँचाई tanα⋅tanβtanα+tanβ km है।
हल

माना B व C दो क्रमागत किलोमीटर के पत्थर हैं तथा उनके बीच H ऊँचाई पर बिन्दु A पर हवाई जहाज है।
∵ B व C के A से अवनमन कोण क्रमश: α व β हैं।
∠ABC = α तथा ∠ACB = β
तथा BC = 1 km
समकोण ∆ADB में, tan α = HBD
⇒ BD = H cot α
इसी प्रकार समकोण ∆ADC से,
DC = H cot β
परन्तु, BD + DC = 1
H cot α + H cot β = 1

प्रश्न 14.
एक झील के तल से h मीटर ऊँचाई पर स्थित एक बिन्दु पर एक बादल का उन्नयन कोण α है तथा झील में उसके प्रतिबिम्ब का अवनमन कोण β है। सिद्ध कीजिए कि झील के तल से बादल की ऊँचाई h(tanβ+tanαtanβ−tanα)m है।
हल
माना PQ झील का तल व झील से h ऊँचाई पर बिन्दु A है।
बिन्दु A से बादल B का उन्नयन कोण ∠BAM = α
तथा बादल के प्रतिबिम्ब C का अवनमन कोण ∠MAC = β