Chapter 9 - त्रिकोणमिति के कुछ अनुप्रयोग (Ex - 9.1)

त्रिकोणमिति के कुछ अनुप्रयोग

प्रश्न 1.
सर्कस का एक कलाकार एक 20 m लम्बी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खम्भे के शिखर से बँधी हुई है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो, तो खम्भे की ऊँचाई ज्ञात कीजिए।
हल

माना AB एक खम्भा है जिसका सिरा B भूमि पर गड़ा है।
खम्भे के शिखर A से एक तनी हुई डोरी AC भूमि पर एक स्थान (बिन्दु) C से बँधी है। डोरी AC की लम्बाई 20 m है।
डोरी भूमि स्तर BC के साथ बिन्दु C पर ∠ACB = 30° बनाती है।
माना AB = h m
दिया है, AC = 20 m
समकोण ΔABC में,

अत: खम्भे की ऊँचाई 10 m है।

प्रश्न 2.
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिन्दु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 m है। पेड़ की ऊँचाई ज्ञात कीजिए।
हल

माना PQ एक पेड़ है जो बिन्दु R से टूटकर भूमि पर गिर गया है।
पेड़ के ऊपरी भाग RP का ऊपरी सिरा P भूमि पर बिन्दु S को छू रहा है।
बिन्दु S की पेड़ से दूरी SQ = 8 m है।
पेड़ का टूटा हुआ भाग PR, भूमि पर बिन्दु S से ∠QSR = 30° बनाता है।
तब, समकोण ΔQSR में,

प्रश्न 3.
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लम्बाई क्या होनी चाहिए?
हल
जब ठेकेदार 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी लगाता है तो उसकी ऊँचाई AB = 1.5 m तथा फिसलनपट्टी का भूमि के साथ कोण ∠ACB = 30° है।
माना इस स्थिति में फिसलनपट्टी की लम्बाई AC m है।

तब, समकोण ΔABC में,
sin 30° = ABAC
⇒ sin 30° = 1.5AC
⇒ 12=1.5AC
⇒ AC = 2 × 1.5 = 3 m
⇒ AC = 3 m
जब ठेकेदार 5 वर्ष से अधिक उम्र के बच्चों के लिए फिसलनपट्टी लगाता है, तो उसकी ऊँचाई A’B’ = 3 m होती है और फिसलनपट्टी भूमि के साथ कोण ∠A’C’B’ = 60° बनाती है।
माना इस स्थिति में फिसलनपट्टी की लम्बाई A’C’ m है।

तब समकोण ΔA’B’C’ में,
sin 60° = A′B′A′C′

अत: 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी की लम्बाई = 3 m तथा इससे अधिक उम्र के बच्चों के लिए फिसलनपट्टी की लम्बाई = 2√3 m

प्रश्न 4.
भूमि के एक बिन्दु से जो मीनार के पाद-बिन्दु से 30 m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए। (√3 = 1.73)
हल
मान लिया, भूमि तल पर एक मीनार AB है जिसकी चोटी (शिखर) A तथा आधार (नीव) B है। मीनार के आधार Bसे 30 m दूर भूमि पर स्थित कोई बिन्दु C है। बिन्दु C से मीनार के शिखर A का उन्नयन कोण ∠ACB = 30° है।
माना मीनार AB की ऊँचाई h m है।

तब, समकोण ΔABC में, tan C = ABBC

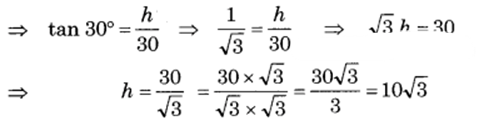
अत: मीनार AB की ऊँचाई = 10√3 m = 10 × 1.73 = 17.3 m

प्रश्न 5.
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिन्दु से बाँध दिया गया और भूमि के साथ डोरी का झकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लम्बाई ज्ञात कीजिए।
हल
माना AX एक क्षैतिज रेखा है जिस पर स्थित एक बिन्दु C से BC = 60 m की ऊँचाई पर एक पतंग B उड़ रही है।
यह पतंग B, क्षैतिज भूमि पर स्थित एक बिन्दु A से तनी हुई डोरी AB द्वारा संयोजित है।
डोरी AB का भूमि के साथ कोण (झुकाव) 60° है।

अत: डोरी की लम्बाई 40√3 या 69.2 m है। (उन्नयन कोण)

प्रश्न 6.
1.5 m लम्बा एक लड़का 30 m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है?
हल
माना PQ एक भवन है जिसकी ऊँचाई 30 m है। भवन के आधार से x m दूर बिन्दु R पर एक लड़का OR खड़ा है, जिसकी ऊँचाई OR = 1.5 m है।

तब, OS || QR
∴ OR = SQ = 1.5 m
माना मीनार की चोटी P का लड़के की आँख O पर उन्नयन कोण ∠POS = 30° है।
तब, PS = PQ – SQ = 30 – 1.5 = 28.5 m
तब, समकोण ∆POS में, tan 30° = PSOS
⇒ 13√=28.5x
⇒ x = 28.5 × √3
⇒ x = 28.5 × 1.732 = 53.496 m
माना लड़का d दूरी चलकर बिन्दु T पर पहुँचता है जहाँ से उसकी आँख का कोण ∠PTS = 60° हो जाता है।
तब, समकोण ∆PTS में,

अत: लड़का भवन की ओर 19√3 m चलकर गया।

प्रश्न 7.
भूमि के एक बिन्दु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हल
माना क्षैतिज भूमितल पर स्थित BQ एक भवन है जिसकी ऊँचाई BQ = 20 m है।
भवन की चोटी के ऊपर एक संचार मीनार BH स्थित है। भवन के आधार Q से किसी दूरी PQ पर एक बिन्दु P है।
बिन्दु P से संचार मीनार के तल का उन्नयन कोण ∠BPQ = 45° तथा शिखर H का उन्नयन कोण ∠HPQ = 60° है।
माना संचार मीनार की भूमि से ऊँचाई HQ है।

तब, समकोण ∆BQP में, tan BPQ = BQPQ
⇒ tan 45° = 20PQ
⇒ 1 = 20PQ
⇒ PQ = 20 m
पुनः समकोण ∆HQP में, tan HPQ = HQPQ
⇒ tan 60° = HB+BQPQ [∵ HQ = HB + BQ]
⇒ √3 = HB+2020 [∵ PQ = 20 m]
⇒ HB + 20 = 20√3
⇒ HB = 20√3 – 20 = 20(√3 – 1) m
अत: मीनार की ऊँचाई = 20(√3 – 1) m

प्रश्न 8.
एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
हल
माना PQ एक x m ऊँची पेडस्टल है जिसकी चोटी P पर एक मूर्ति PS लगी है। मूर्ति की ऊँचाई PS = 1.6 m है।
क्षैतिज भूमि पर स्थित एक बिन्दु R से मूर्ति के ऊपरी सिरे S का उन्नयन कोण ∠QRS = 60° है तथा इसी बिन्दु R से पेडस्टल के शिखर P का उन्नयन कोण ∠PRQ = 45° है।
मूर्ति PS की लम्बाई 1.6 m है।

अत: मूर्ति की ऊँचाई 0.8(√3 + 1) m है।

प्रश्न 9.
एक मीनार के पाद-बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
हल
माना AB एक मीनार है जिसकी ऊँचाई 50 m है। मीनार के पाद-बिन्दु B से एक भवन CD की चोटी D का उन्नयन कोण 30° है, जबकि भवन के आधार-बिन्दु C से मीनार की चोटी A का उन्नयन कोण 60° है। मीनार के आधार B से भवन के आधार C की दूरी BC है।
माना भवन की ऊँचाई CD = x m

प्रश्न 10.
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान ऊँचाई वाले दो खम्भे लगे हुए हैं। इन दोनों खम्भों के बीच सड़क के एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खम्भों की ऊँचाई और खम्भों से बिन्द की दूरी ज्ञात कीजिए।
हल
माना, PA तथा QB समान ऊँचाई h m के दो खम्भे हैं जो सड़क की चौड़ाई AB के सिरों क्रमश: A व B पर स्थित हैं।
खम्भों की सीध में सड़क के किसी बिन्दु R से दोनों खम्भों के शिखर क्रमश: 60° व 30° के उन्नयन कोण बनाते हैं।
सड़क की चौड़ाई AB = 80 m तथा माना बिन्दु R की पहले खम्भे PA से दूरी x m है।
अत: बिन्दु R की खम्भे QB से दूरी = (80 – x) m

समीकरण (1) व (2) से,
√3x = 80−x3√
⇒ 3x = 80 – x
⇒ 4x = 80 m
⇒ x = 20 m
समीकरण (1) में x का मान रखने पर,
h = √3 × 20 = 1.73 × 20 = 34.60 m
अतः खम्भे की ऊँचाई = 34.60 m और पहले खम्भे से प्रेक्षण बिन्दु की दूरी = 20 m
तथा दूसरे खम्भे से प्रेक्षण बिन्दु की दूरी = 80 – 20 = 60 m.

प्रश्न 11.
एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिन्द को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्द से टॉवर के शिखर का उन्नयन कोण 30° है (चित्र देखिए)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

हल
माना BC चौड़ाई की एक नहर है जिसके एक तट B पर एक टीवी टॉवर AB खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक बिन्दु C से टॉवर के शिखर का उन्नयन कोण ∠ACB = 60° है। इसी तट पर इस बिन्दु से 20 m दूर तथा बिन्दु C और टॉवर के आधार B को मिलाने वाली रेखा की सीध में एक बिन्दु D है। बिन्दु D से टॉवर के शिखर का उन्नयन कोण 30° है।
माना टॉवर AB की ऊँचाई h m तथा नहर की चौड़ाई BC = x m है।
तब, समकोण ΔABC में,

समीकरण (1) में x का मान रखने पर, h = 10√3 m
अत: टीवी टॉवर की ऊँचाई = 10√3 m तथा नहर की चौड़ाई = 10 m

प्रश्न 12.
7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
हल
माना AB एक केबल टॉवर है और उसी धरातल में एक भवन CD है जिसकी ऊँचाई 7 m है।
भवन के शिखर C से क्षैतिज धरातल के समान्तर एक रेखा CE है। भवन के शिखर C से केबल टॉवर के शिखर A का उन्नयन कोण ∠ACE = 60° है और केबल टॉवर के पाद B का अवनमन कोण ∠ECB = 45° है।

∵ DB || CE और ∠DCE = 90°
तथा ∠EBD = 90° ⇒ CD || EB
चतुर्भुज CDBE एक समान्तर चतुर्भुज है।
∴ EB = CD ⇒ EB = 7 m
अब समकोण ΔBEC में, tan 45° = EBCE
⇒ 1 = 7CE
⇒ CE = 7 m
पुनः समकोण ΔAEC में, tan 60° = AECE
⇒ √3 = AE7
⇒ AE = 7√3 m
तब, केबल टॉवर AB की ऊँचाई = AE + EB = 7√3 + 7 = 7(√3 + 1) m
अत: केबल टॉवर की ऊँचाई 7(√3 + 1) m है।

प्रश्न 13.
समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
हल
माना 75 m ऊँचे एक प्रकाश स्तम्भ PQ के शिखर P से, A और B जहाजों के अवनमन कोण क्रमश: 30° और 45° हैं।

∴ ∠SPA = 30° = ∠PAQ (एकान्तर कोण)
तथा ∠SPB = 45° = ∠PBQ (एकान्तर कोण)
माना जहाजों के बीच की दूरी AB = x m
तब, समकोण ΔPQB में,

प्रश्न 14.
1.2 m लम्बी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है। इस अन्तराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

हल

प्रश्न 15.
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एकसमान चाल से जाता है। छ: सेकण्ड बाद कार का अवनमन कोण 60° हो गया। इस बिन्दु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
हल
माना BCQ एक सीधा राजमार्ग है जिसके किसी बिन्दु Q पर खड़ी मीनार की ऊँचाई OQ है। एक प्रेक्षक मीनार के शिखर बिन्दु 0 पर बैठा देखता है कि एक कार B का अवनमन कोण 30° है जिससे ∠OBQ = 30° है। प्रेक्षक 6 सेकण्ड बाद देखता है कि कार का अवनमन कोण 60° है जिससे ∠OCQ = 60° है।
समकोण ∆OQB में,

∴ CQ दूरी तय करने में लगने वाला समय = 12 × BC दूरी तय करने में लगा समय
= 12 × 6 सेकण्ड
= 3 सेकण्ड
अत: कार को मीनार के पाद तक पहुँचने में लगने वाला समय = 3 सेकण्ड

प्रश्न 16.
मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 m है।
हल
माना AB एक मीनार है जिसकी ऊँचाई h है। मीनार के आधार B के दोनों ओर B से क्रमश: 9 m और 4 m दूरियों पर दो बिन्दु P और Q स्थित हैं।
यदि बिन्दु P से मीनार की चोटी का उन्नयन कोण हो तो Q से मीनार की चोटी का उन्नयन कोण θ का कोटिपूरक (90° – θ) होगा।